Matemática para TJ-SP: Noções de Geometria

Confira neste artigo as principais noções de geometria, da disciplina de Matemática, para o concurso do TJ-SP.

Este artigo é para você que vai prestar o concurso do TJ-SP e está receoso com a disciplina de Matemática. Venha conosco e aprenda os principais tópicos desta disciplina para o seu concurso. E o artigo de hoje é sobre Noções de Geometria, para o TJ-SP.

Vale destacar que o TJ-SP está com dois editais abertos, para o cargo de Escrevente, com remuneração inicial podendo chegar a R$ 7.209,16.

Vamos lá!

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.

Perímetro

Vamos começar o nosso artigo com um dos assuntos mais básicos da geometria, o perímetro.

Perímetro é a medida do contorno de uma forma bidimensional. Em outras palavras, é a soma do comprimento de todos os lados de uma forma geométrica.

Assim, em um quadrado de lado tamanho L, o seu perímetro será L+ L+ L+ L = 4L.

Já o perímetro de um triângulo equilátero de lado L será L + L + L = 3L.

No caso de um círculo de raio R, o seu perímetro é chamado de circunferência, sendo ele calculado por 2πR.

PI: O valor de π pode ser definido, para cálculos em prova, como 3,14.

Área

A área, por sua vez, é a medida da superfície da figura geométrica, geralmente calculada por mm², cm², m², km².

Cada forma geométrica possui a sua maneira de calcular a sua área. Iremos analisar abaixo as áreas da principais formas geométricas.

No caso de um retângulo, de altura a e base b, como visto abaixo, a sua área é a multiplicação desses dois valores: a x b

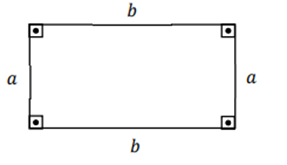
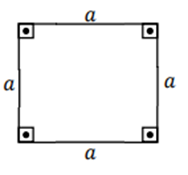
No caso de um quadrado, o cálculo é similar ao de cima. Como os seus lados são iguais, então a sua área é a x a = a².

No caso de uma circunferência de raio r, temos que a sua área é πr².

Por fim, vamos analisar a área do triângulo.

O triângulo pode ser de três tipos:

Equilátero: todos os lados iguais.
Isósceles: dois lados iguais e um diferente.
Escaleno: três lados diferentes.

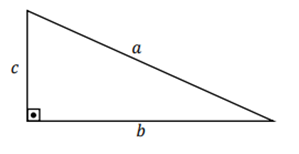
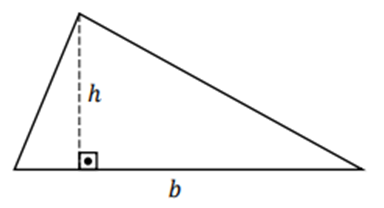
Além disso, há também os chamados triângulos retângulos, que são aqueles que possuem um ângulo de 90º, como na figura abaixo:

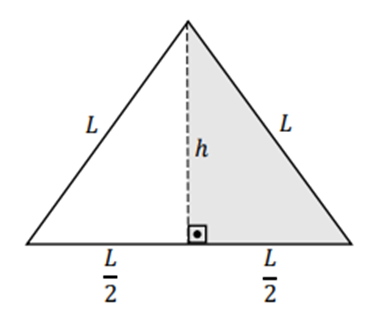
A fórmula geral para a área do triângulo é:

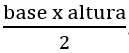
Assim, a área de um triângulo retângulo, como o visto acima, será:

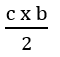
No caso de um triângulo não retângulo, como o visto abaixo, a sua área será:

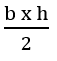
Contudo, quando houver um triângulo equilátero, é possível encontrar uma fórmula específica, derivada da fórmula geral acima:

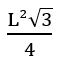
Volume

Os volumes são calculados em relação a formas tridimensionais, também chamados de poliedros, como cubos, esferas pirâmides, entre outros.

Vamos listar as fórmulas dos volumes das principais figuras geométricas, para a sua prova.

Primeiramente, vamos aprender a calcular o volume de prismas.

Prismas são poliedros que possuem duas bases paralelas distintas, como as figuras abaixo:

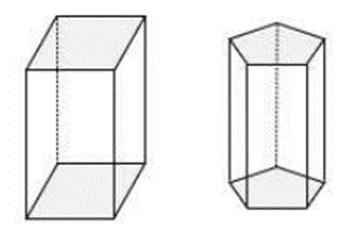
Assim, um paralelepípedo e um cubo também são prismas.

Para calcular o volume dessas figuras, usa-se a fórmula área da base x altura.

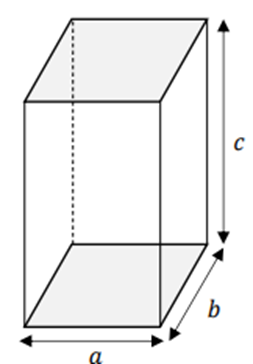
Dessa maneira, o volume de um paralelepípedo mostrado abaixo é a x b x c.

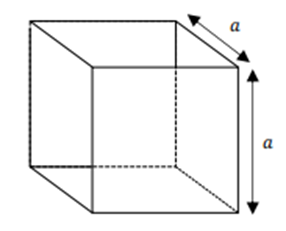
Já o volume de um cubo de lado a é a x a x a = a³, como visto abaixo:

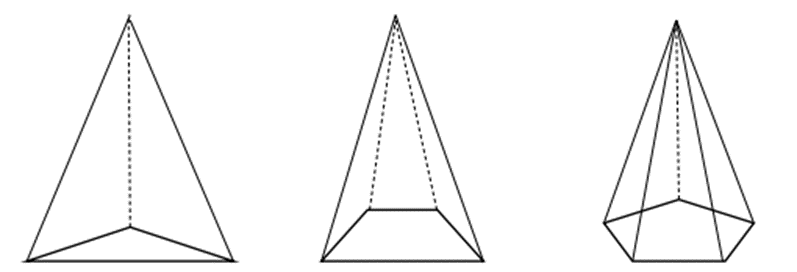
Em relação às pirâmides, temos que os seus volumes são:

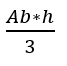
Ab é a área da base, sendo h a sua altura.

Essa fórmula é válida para pirâmides de qualquer forma geométrica da base, como visto abaixo:

Por fim, o volume de uma esfera de raio R é calculado por:

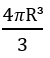
Teorema de Pitágoras

O Teorema de Pitágoras, um dos mais famosos teoremas da matemática, diz o seguinte:

“A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”

Mas o que são catetos e hipotenusa?

Bom, primeiramente, devemos destacar que este teorema é utilizado em triângulos retângulos, como o visto abaixo:

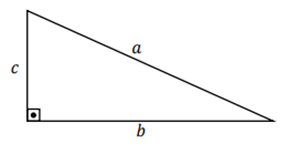
Assim, os catetos são lados do triângulo adjacentes ao ângulo de 90º graus, ou seja, b e c, enquanto que a hipotenusa é o lado oposto ao ângulo de 90º, ou seja, o lado a.

Dessa maneira, o que o Teorema de Pitágoras diz é que a² = b² + c².

Assim, sabendo o comprimento de dois dos três lados de um triângulo retângulo, é possível encontrar o comprimento do terceiro lado, utilizando a fórmula citada.

Finalizando

Pessoal, finalizamos o nosso artigo noções de geometria, da disciplina de Matemática, para o concurso do TJ-SP.

Esperamos que tenham gostado.

Caso queira se preparar para chegar competitivo nesta prova, invista nos cursos para o TJ-SP do Estratégia Concursos. Lá você encontrará aulas completas e detalhadas, com os melhores professores do mercado, de todos os tópicos exigidos no edital deste concurso.

Conheça também o Sistema de Questões do Estratégia. Afinal, a única maneira de consolidar o conteúdo de maneira satisfatória é através da resolução de questões.

Bons estudos a todos e até a próxima!