Resumo de Probabilidade para ISS-BH – Estatística

Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo de Probabilidade para ISS-BH.

Trata-se de um tema muito ligado ao que vimos na Análise Combinatória, assim caso ainda não tenha estudado o tema, aconselhamos revisá-lo primeiro.

Preparado (a)? Vamos lá.

Conceitos Gerais

Iniciemos o Resumo de Probabilidade para ISS-BH pelos conceitos gerais/iniciais.

A Teoria da Probabilidade estuda fenômenos aleatórios (incertos). O exemplo clássico é o lançamento de um dado ou de uma moeda.

Mesmo que os resultados sejam incertos, caso o experimento seja repetido diversas vezes é possível encontrar um padrão (exemplo: 50% cara e 50% coroa).

Assim, podemos resumir da seguinte forma

Fenômenos aleatórios:

• Podem ser repetidos indefinidamente, sob condições inalteradas;
• Apresentam resultado incerto, porém com um padrão conhecido

Espaço Amostral: conjunto de todos os resultados possíveis. No caso da moeda {cara, coroa}, no caso do dado não viciado {1, 2, 3, 4, 5, 6}.

Já o ponto amostral é cada resultado possível. Exemplo: no lançamento de duas moedas, há 4 pontos amostrais.

Evento: qualquer subconjunto do Espaço Amostral. Exemplo: No lançamento de 2 moedas para que ambas tenham o mesmo resultado em A = {(CARA, CARA), (COROA, COROA)}

Definição clássica de probabilidade

Dando continuidade ao Resumo de Probabilidade para ISS-BH, vejamos a definição clássica de probabilidade.

Na definição clássica de probabilidade basicamente temos os casos favoráveis pelos casos totais (Quero/total).

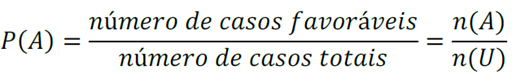
Obs.: Para que se utilize a definição clássica “sem nenhum ajuste”, é imprescindível que a probabilidade de cada ponto amostral seja igual.

Exemplo: (FGV/2019 – Prefeitura de Angra dos Reis/RJ) Uma pesquisa feita com os alunos de uma sala mostrou que 7 alunos torcem pelo Flamengo, 6 pelo Vasco, 5 pelo Fluminense, 4 pelo Botafogo e 3 não torcem por time nenhum. Escolhendo ao acaso um dos alunos dessa turma, a probabilidade de que ele seja torcedor do Vasco é de

P = 6 / (7 + 6 + 5 + 4 + 3)

P = 6 / 25

P = 24%

Teorema da União e da Interseção

Agora vejamos sobre a União e a Intersecção de dados.

Vamos tratar inicialmente de dois casos “extremos”.

• Eventos exaustivos: Quando a união de eventos corresponde a todo o Espaço Amostral. -> A = {1, 2}; B = {3, 4}; A união dos conjuntos {1, 2, 3, 4}
• Eventos Mutuamente Excludentes: Quando não há intersecção (conjunto vazio). -> A = {1, 2}; B = {3, 4}; A intersecção é vazia {}

Entretanto não é o que os exercícios costumam abordar, geralmente temos elementos em comum.

Probabilidade da União – caso geral

Vejamos a probabilidade da União.

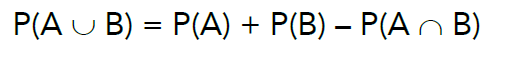
Repare que precisamos subtrair a interseção para retirar elementos repetidos.

Exemplo: (FGV/2018 – ALE/RO) Dois eventos A e B ocorrem, respectivamente, com 40% e 30% de probabilidade. A probabilidade de que A ocorra ou B ocorra é 50%. Assim, a probabilidade de que A e B ocorram é igual a

P = 40 + 30 – 50

P = 20%

Isso vale inclusive para a União de mais de dois conjuntos, em uma questão de concurso dificuldade será cobrado mais de 3 conjuntos, assim é válido conhecer também a seguinte fórmula:

União de Eventos mutuamente excludentes

Já a União de Eventos mutuamente excludentes basta somar P(A) + P(B), afinal não há intersecção entre A e B.

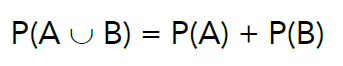
Teorema do Evento Complementar

Prosseguindo no Resumo de Probabilidade para ISS-BH, agora vejamos sobre o Teorema do Evento Complementar.

O evento complementar corresponde a todos os elementos do Espaço Amostral que não pertencem a tal evento.

Podemos representar a partir da seguinte fórmula:

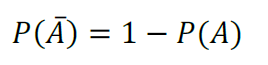
Exemplo: (2019 – Prefeitura de Palhoça/SC) Uma urna tem dez bolas vermelhas, três azuis e duas pretas. Qual é a probabilidade de sortearmos uma bola que não seja da cor vermelha?

Probabilidade de sortearmos a bola vermelha é:

P(V) = 10 / (10 + 3 + 2)

P(V) = 10 / 15

Logo a probabilidade não sortearmos uma bola vermelha, ou seja, o evento complementar é

P (nV) = 1 – 10/15

P (nV) = 5/15

P (nV) = 1/3

Axiomas/Propriedades de Probabilidade

Axiomas são verdades “absolutas”, ou seja, verdades básicas/elementares.

• 1. A probabilidade de A igual ou maior que 0

A probabilidade de um evento é sempre maior que 0, em outros termos, não há probabilidade negativa.

• 2. P(U) = 1

Ou seja, a probabilidade do espaço amostral é sempre 100%

Apesar de fácil entendimento, lembrar desses conceitos pode ajudá-los.

Probabilidade Condicional

A probabilidade condicional ocorre quando sabemos que um evento já ocorreu.

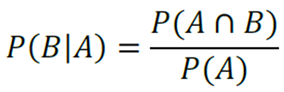
Exemplo: (FCC/2018 – Banrisul/RS) Em uma empresa com 400 funcionários, 30% ganham acima de 5 Salários Mínimos (S.M.). O quadro de funcionários dessa empresa é formado por 180 homens e 220 mulheres, sendo que 160 mulheres ganham no máximo 5 S.M. Escolhendo aleatoriamente 1 funcionário dessa empresa e verificando que é homem, a probabilidade de ele ganhar mais do que 5 S.M. é igual a

Dizemos que a probabilidade condicional um evento já ocorreu, correto? Nesse caso a nossa condição (evento que já ocorreu) é “verificando que é homem”, assim temos que.

Dos 400 funcionários, 120 ganham acima de 5SM (30% de 400) e desses 120, 60 são mulheres (220 – 160), logo os outros 60 são homens, assim:

P = 60 / 180

P = 1/3

Eventos Independentes

Os Eventos independentes são aqueles que não influenciam uns nos outros, pois o resultado de um não influencia o resultado do outro.

Ao lançar um dado, independentemente do número que cair, no próximo lançamento haverá a mesma probabilidade para todos os 6 números possíveis.

Assim, podemos dizer que a probabilidade de um evento ocorrer (2 no dado) dada uma condição (ter saído 3 anteriormente) é a própria probabilidade do lançamento (1/6).

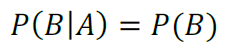
Uma informação muito importante é a teoria da multiplicação para eventos independentes.

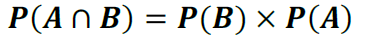
Segue a dica dos nosso professores:

“Para eventos independentes, a probabilidade da interseção (conectivo E) é igual ao produto das probabilidades; e a probabilidade da união (conectivo OU) é igual à soma das probabilidades.”

Exemplo: (CESPE/2019 – TJ/AM) Em um espaço de probabilidades, as probabilidades de ocorrerem os eventos independentes A e B são, respectivamente, P(A) = 0,3 e P(B) = 0,5.

P = 0,3 x 0,5

P = 0,15

Considerações Finais

Pessoal, chegamos ao final do Resumo sobre Resumo de Probabilidade para ISS-BH. Espero que o artigo tenha sido efetivo para seu aprendizado.

Obviamente trata-se de um resumo apenas com os pontos principais da matéria, tendo outros temas correlacionados como a Teorema da Probabilidade Total, Teorema de Bayes e etc., assim não deixe de acompanhar as aulas para o aprofundamento necessário.

Ainda, ressaltamos mais uma vez a importância de praticar por exercícios, assim faça muitas questões pelo nosso sistema de questões.

Sistema de Questões (SQ) – Estratégia Concursos

Gostou do artigo? Não deixe de seguir

https://www.instagram.com/resumospassarin/

Cursos e Assinaturas

Até mais e bons estudos!