Regra de Três – Saiba Como calcular e não erre mais em prova!

Regra de Três é um dos assuntos mais importantes de toda a Matemática Básica, que nos permite resolver um grande número de problemas. Alguns problemas são muito simples; outros, bem mais complexos.

Comecemos do básico. Suponha que Pedro produz 2 sapatos por dia. Quantos sapatos ele produzirá em 2 dias? Simples. Em 2 dias, ele produzirá 4 sapatos.

Mesmo que não tenha percebido, você acabou usando a regra de três para resolver esse problema. Foi simples, não é?

Basicamente, regra de Três é um método para resolver problemas que envolvem grandezas direta ou inversamente proporcionais. É justamente por isso que é utilizada para resolver problemas de muitos assuntos em Matemática e também muitos problemas de Física e Química.

Regra de Três Simples e Composta

Na regra de três simples, três valores são conhecidos e temos como objetivo encontrar um quarto valor. Na regra de três composta, são conhecidos mais de três valores.

Entretanto, isso pouco importa. Os métodos para resolver a regra de três simples e a regra de três composta são exatamente os mesmos.

Primordialmente, o primeiro passo para resolver problemas de regra de três é construir uma tabela agrupando as grandezas de mesma espécie em colunas.

Em segundo lugar, devemos ainda manter na mesma linha as grandezas de espécie diferentes em correspondência. Vejamos um exemplo!

Regra de Três – Exemplo Resolvido

Exemplo: Em uma fábrica, 400 peças são produzidas diariamente por 10 funcionários que trabalham 8 horas por dia. Quantas peças seriam produzidas diariamente por 15 funcionários que trabalham 6 horas por dia, considerando que a dificuldade para produzir as peças dobrou?

Neste exemplo, teremos 4 colunas visto que são 4 grandezas envolvidas: o número de peças, a quantidade de funcionários, o número de horas que cada funcionário trabalha diariamente e a dificuldade de produção. Vamos colocar estas grandezas no cabeçalho da tabela.

Temos duas situações para comparar na regra de três.

Na primeira situação, 400 peças são produzidas diariamente por 10 pessoas que trabalham 8 horas por dia. Esta situação em que todos os valores são conhecidos ficará na primeira linha da tabela.

Além disso, na regra de três, temos a grandeza “dificuldade”. Como colocar isto na tabela?

Ora, o problema disse que a dificuldade dobrou, então vamos colocar um valor qualquer para a dificuldade na primeira situação da regra de três.

Na segunda situação, a dificuldade será o dobro. Podemos colocar 1 e 2, ou 10 e 20, ou 100 e 200. Tanto Faz.

Vou colocar dificuldade 1 na primeira situação da regra de três e dificuldade 2 na segunda situação.

Na segunda situação da regra de três, há 15 funcionários que trabalham 6 horas por dia. Sabemos ainda que a dificuldade dobrou. Queremos saber quantas peças serão produzidas diariamente. Esta situação ficará na segunda linha da tabela.

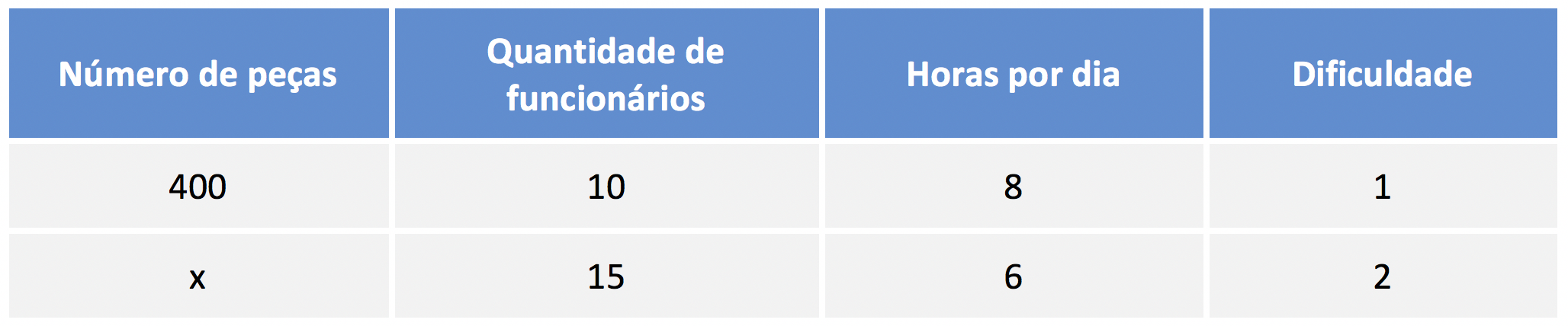
Para resolver este problema de regra de três, vamos comparar as grandezas conhecidas (quantidade de funcionários, horas/dia, dificuldade) com a grandeza desconhecida (número de peças).

Para podermos comparar as grandezas da regra de três, vamos colocar uma seta para baixo na coluna da grandeza desconhecida.

Sempre é assim! Na coluna da grandeza desconhecida (onde tem o “x”), colocamos uma seta para baixo.

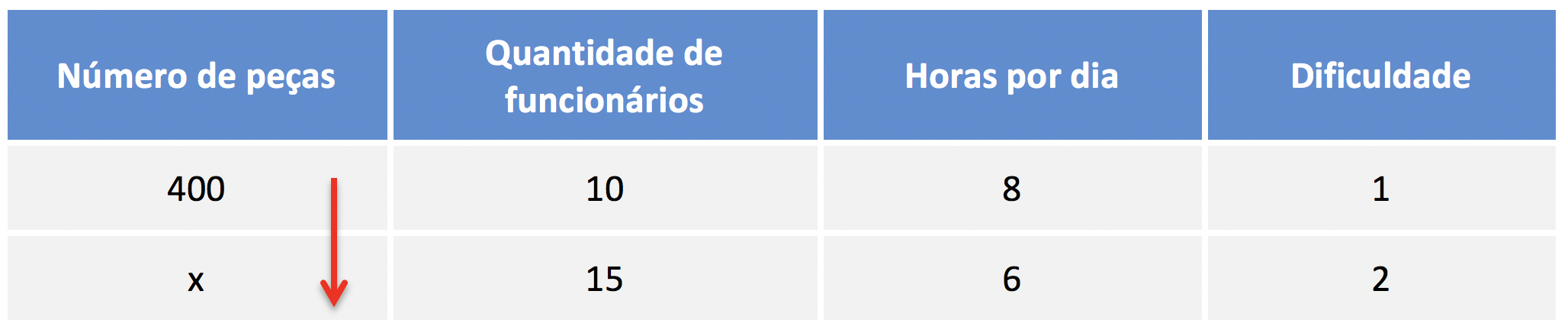
Vamos agora comparar as grandezas da regra de três e decidir se são diretamente ou inversamente proporcionais.

Quando as grandezas forem diretamente proporcionais, colocaremos uma seta para baixo. Quando as grandezas forem inversamente proporcionais, colocaremos uma seta para cima.

Afinal, como sabemos se são direta ou inversamente proporcionais? É muito simples.

Você vai observar se a grandeza conhecida da regra de três aumentou ou diminuiu. Depois, vai se perguntar o que acontece com a grandeza desconhecida.

Se as duas grandezas aumentam ou se as duas grandezas diminuem, elas serão diretamente proporcionais.

Por analogia, se uma grandeza aumenta enquanto a outra diminui, as grandezas são inversamente proporcionais.

Voltemos à nossa tabela da Regra de Três.

Vamos comparar a quantidade de funcionários com o número de peças.

Observe que a quantidade de funcionários aumentou. Ora, se temos mais funcionários trabalhando, então a quantidade de peças produzidas também aumentará.

Como as duas grandezas aumentaram, então elas são diretamente proporcionais. A seta da quantidade de funcionários ficará voltada para baixo também na tabela da regra de três.

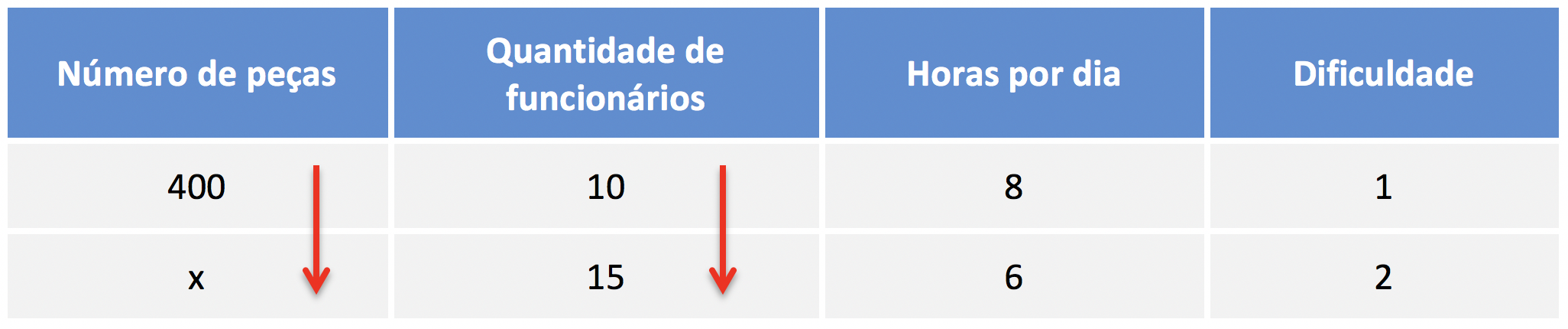
Seja como for, vamos agora comparar a quantidade de horas trabalhadas por dia com o número de peças produzidas.

Observe que a quantidade de horas trabalhadas diminuiu. Como os funcionários estão trabalhando menos horas por dia, a quantidade de peças produzidas diariamente vai diminuir.

Como as duas grandezas diminuíram, as grandezas são diretamente proporcionais. A seta fica para baixo.

Lembre-se: quando as duas grandezas aumentam ou quando as duas diminuem, as grandezas são diretamente proporcionais. Por consequência, a seta fica voltada para baixo.

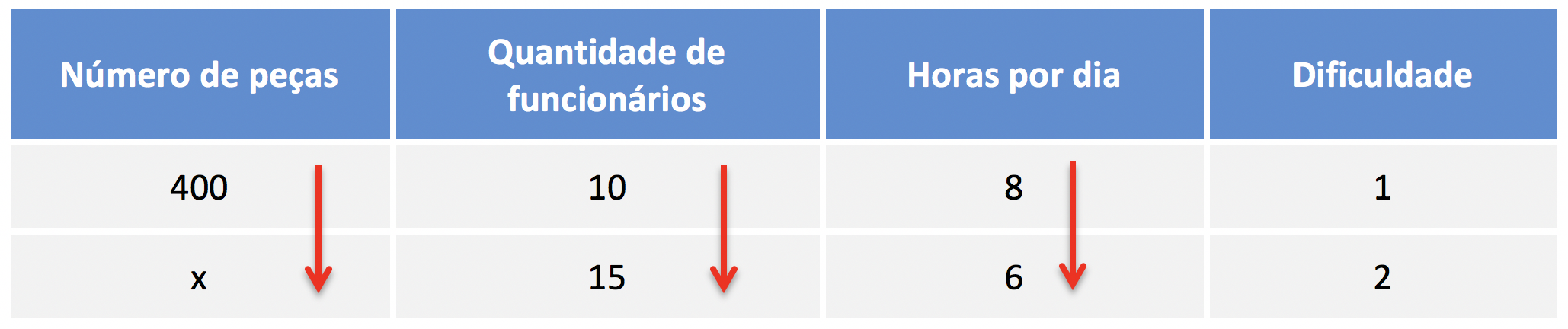
Finalmente, vamos comparar a dificuldade com o número de peças. A dificuldade aumentou. Como o processo para produzir peças está mais difícil, o número de peças produzidas tende a diminuir.

Então, como uma grandeza está aumentando e a outra está diminuindo, as grandezas são inversamente proporcionais. Dessa forma, a seta fica voltada para cima.

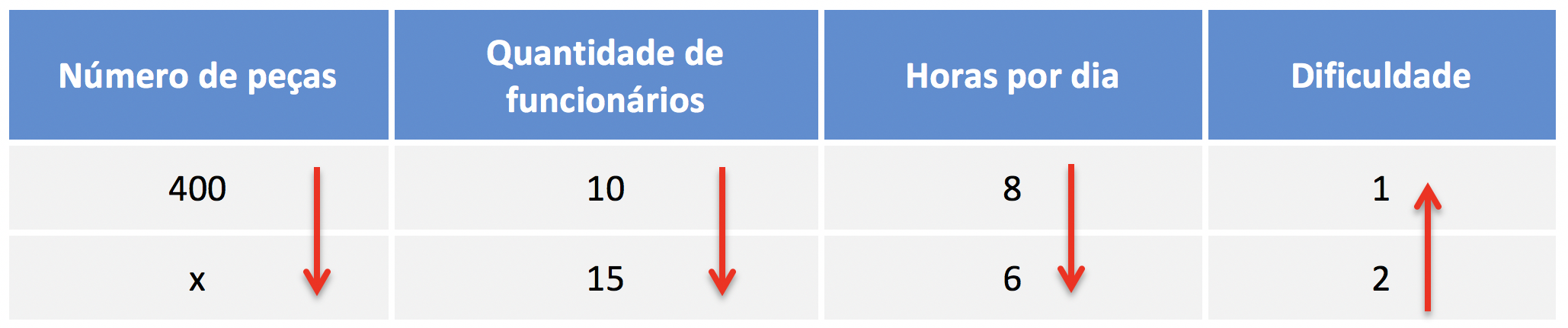
Como montar a equação da Regra de Três

Por fim, vamos montar a equação da regra de três. Formaremos frações e, para tanto, devemos seguir o sentido das setas.

Quando a seta está voltada para baixo, mantemos o sentido numerador/denominador.

Nesse sentido, quando a seta está para cima, devemos inverter a fração.

Do lado esquerdo da equação, vamos colocar a fração da grandeza desconhecida.

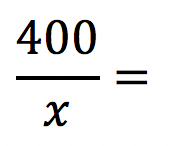
Logo depois, do lado esquerdo, vamos colocar o PRODUTO das outras frações, ou seja, vamos multiplicar as outras frações obedecendo o sentido das setas.

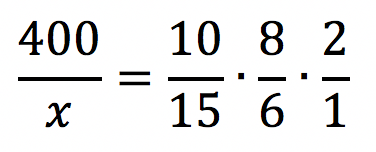
Só para exemplificar, observe que a única fração invertida foi a última, em que a seta ficou para cima.

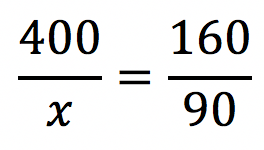
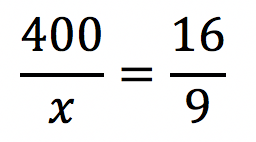
Logo depois, vamos aplicar a propriedade fundamental das proporções, isto é, o produto dos meios é igual ao produto dos extremos.

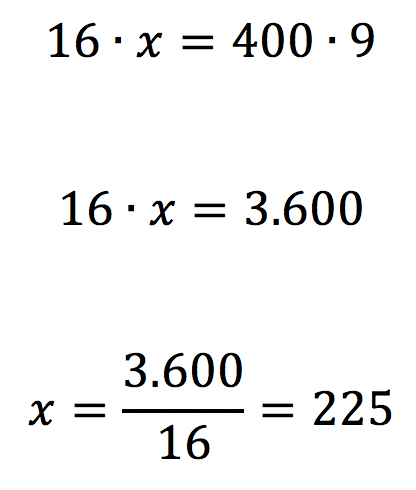
Serão produzidas 225 peças diariamente.

Simplificando a Regra de Três

Às vezes, simplifico os números na própria tabela.

Entretanto, sugiro que faça isso apenas quando os números são muito grandes e é possível visualizar de imediato a possibilidade de simplificação, para que você trabalhe com números menores.

Perceba que a simplificação será sempre com números na mesma coluna da tabela.

Observe, por exemplo, a tabela do exemplo anterior.

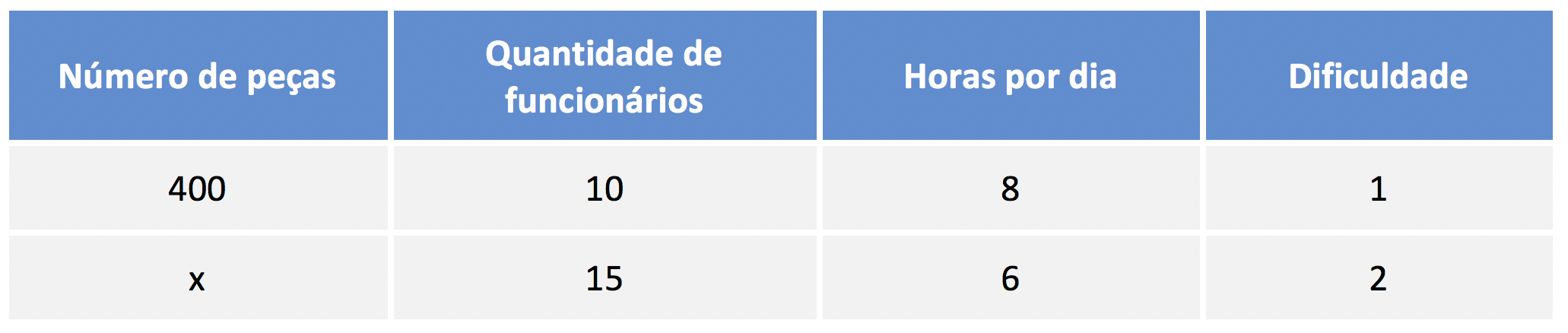
Só para ilustrar, para acelerar a resolução da regra de três, poderíamos ter simplificado a segunda coluna por 5 e a terceira coluna por 2.

Raciocínio Lógico para Concursos – Materiais Gratuitos

Exercícios de porcentagem