Raciocínio Lógico TRT/PE – prova resolvida e gabarito
Caros alunos,
Vejam a seguir a minha correção das questões de Raciocínio Lógico das provas do TRT/PE para os cargos de Técnico e de Analista Judiciário, bem como o gabarito. Espero que tenham mandado muito bem!
TÉCNICO JUDICIÁRIO – PROVA DE RACIOCÍNIO LÓGICO RESOLVIDA
FCC – TRT/PE – 2018) Na prateleira de uma estante estão dispostos 10 livros de direito, 12 livros de economia e 15 livros de administração. O menor número de livros que se devem retirar ao acaso dessa prateleira para que se tenha certeza de que dentre os livros retirados haja um de direito, um de economia e um de administração é igual a
(A) 26.
(B) 23.
(C) 27.
(D) 28
(E) 29.
RESOLUÇÃO:
Veja que eu posso dar o “azar” de os primeiros 15 livros que eu pegar serem de administração, e os 12 livros seguintes serem de economia. Ou seja, é possível pegar 27 livros e, mesmo assim, não ter um de cada tipo. Porém, mesmo neste pior cenário, o vigésimo oitavo livro que pegar será de direito e, com isso, terei um de cada tipo. Portanto, pegando 28 livros , temos certeza de que há pelo menos um de cada tipo.
Resposta: D
FCC – TRT/PE – 2018) O maior valor monetário, em reais, de três notas de valores diferentes e três moedas de valores diferentes é igual a
(A) 81,75.
(B) 171,75
(C) 110,50.
(D) 171,25.
(E) 171,60.
RESOLUÇÃO:
As maiores notas são de 100 + 50 + 20 = 170 reais. Já as maiores moedas são 1,00 + 0,50 + 0,25 = 1,75 real. Somando tudo, temos 171,75 reais.
Resposta: B
FCC – TRT/PE – 2018) Em relação aos 31 dias de um mês, Fernando, Geraldo e Hélio folgaram, respectivamente, nos dias que são “múltiplos de 6”, “divisores de 12” e “múltiplos de 3 e divisores de 30”. Nesse mês, os três trabalharam juntos em um total de
(A) 19 dias.
(B) 21 dias
(C) 23 dias.
(D) 22 dias.
(E) 20 dias.
RESOLUÇÃO:
Anotando todos os dias de 1 a 31, temos:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31
Os múltiplos de 6 são 6, 12, 18, 24 e 30. Retirando-os, temos:
1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 25, 26, 27, 28, 29, 31
Desses, números, os divisores de 12 são 1, 2, 3, 4. Retirando-os, temos:
5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 25, 26, 27, 28, 29, 31
Devemos ainda tirar os números que, ao mesmo tempo, são múltiplos de 3 e divisores de 30. Isso só ocorre com o 15. Ficamos com:
5, 7, 8, 9, 10, 11, 13, 14, 16, 17, 19, 20, 21, 22, 23, 25, 26, 27, 28, 29, 31
Temos, ao todo, 21 dias em que eles trabalharam juntos.
Resposta: B
FCC – TRT/PE – 2018) Exatamente ¼ das vagas de uma faculdade são destinadas aos cursos de humanas, e exatamente 1/8 das vagas destinadas aos cursos de humanas são do período noturno. Sabendo-se que o total de vagas dessa faculdade é um número inteiro positivo entre 420 e 470, então o número de vagas dessa faculdade destinadas aos cursos de humanas é igual a
(A) 108.
(B) 124.
(C) 112
(D) 120.
(E) 104.
RESOLUÇÃO:
Sendo V vagas ao todo, sabemos que V/4 são de humanas. 1/8 disto são vagas noturnas, ou seja,
Vagas noturnas de humanas = (1/8) x (V/4) = V/32
O número de vagas deve ser um número inteiro. Logo, V deve ser divisível por 32, e estar entre 420 e 470. Se dividirmos 470 por 32, teremos resto 22. Isto significa que o 470 é 22 unidades maior do que um múltiplo de 32. Ou seja, 470 – 22 = 448 é múltiplo de 32. Este é o número de vagas. O número de vagas de humanas é V/4 = 448/4 = 112.
Resposta: C
FCC – TRT/PE – 2018) Em um determinado departamento, todos os funcionários são ou advogados, ou economistas, ou advogados e economistas. Sabe-se que 5 funcionários são apenas economistas, e que 15 funcionários são advogados, sendo que parte destes também são economistas. Se 45% dos funcionários desse departamento são advogados e economistas, então o número de funcionários do departamento que são apenas advogados é igual a
(A) 7.
(B) 8.
(C) 4.
(D) 5.
(E) 6
RESOLUÇÃO:
Veja que temos 15 funcionários que são advogados (sendo que parte deles é também economista). Somando-os com aquelas pessoas que são SOMENTE economistas (5), temos o total 15+5 = 20 pessoas. Sabemos que 45% deste total tem ambas as profissões, ou seja, 45% x 20 = 0,45 x 20 = 9 pessoas tem ambas as profissões.
Logo, são SOMENTE advogados 15 – 9 = 6 pessoas.
Resposta: E
FCC – TRT/PE – 2018) Uma mercadoria comprada por R$ 1.400,00 será vendida com lucro de 20% sobre o preço de compra acrescido com 15% de imposto. Nessas condições, o preço de venda dessa mercadoria, deve ser igual a
(A) R$ 1.540,00.
(B) R$ 1.442,00.
(C) R$ 1.932,00
(D) R$ 1.890,00.
(E) R$ 1.952,00.
RESOLUÇÃO:
Dando um aumento de 20%, chegamos em 1400 x 1,20 = 1680 reais. Com um aumento de 15%, chegamos em 1680 x 1,15 = 1932 reais. Este é o valor final.
Resposta: C
FCC – TRT/PE – 2018) Amanda, Manuela, Patrícia, Olívia e Daniela fizeram uma mesma prova, cuja nota mais alta, dentre elas, foi 18. Amanda obteve a metade da nota conquistada por Manuela. Patrícia tirou nota equivalente à média aritmética das notas de Daniela e Manuela. Olívia obteve a mesma nota que Daniela, e o triplo da nota de Amanda. A segunda maior nota dentre as cinco pessoas foi igual a
(A) 15 e obtida por Patrícia
(B) 16,5 e obtida por Patrícia.
(C) 12 e obtida por Manuela.
(D) 16,5 e obtida por Manuela.
(E) 15 e obtida por Olívia e Daniela.
RESOLUÇÃO:
Chamando de A, M, D, O e P as notas de cada mulher, temos:
- Amanda obteve a metade da nota conquistada por Manuela: A = M/2, ou seja, M = 2A.
- Patrícia tirou nota equivalente à média aritmética das notas de Daniela e Manuela: P = (D+M)/2
- Olívia obteve a mesma nota que Daniela, e o triplo da nota de Amanda: O = D = 3A.
Da segunda equação, veja que:
P = (D+M)/2 = (3A + 2A)/2 = 5A/2 = 2,5A
Portanto, temos notas de valores:
- 3A
- 2,5A
- 2A
- A
A maior nota é 3A, que vale 18, ou seja:
3A = 18
A = 6
Assim, a segunda maior nota dentre as cinco pessoas foi igual a 2,5A = 2,5×6 = 15. Esta é a nota de Patrícia.
Resposta: A
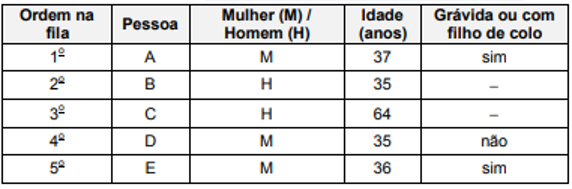
FCC – TRT/PE – 2018) Uma fila será organizada com base em três critérios, que são:
- mulheres grávidas ou com criança de colo ficam à frente das demais pessoas;
- as pessoas mais velhas ficam à frente de outras pessoas de idade menor que a sua;
- mulheres ficam à frente dos homens.
Sabe-se que o critério 1 prevalece em relação ao 2 e ao 3, e que o critério 2 prevalece em relação ao critério 3.
Antes do uso desse critério de organização, cinco pessoas já estavam em uma fila de acordo com a ordem apresentada na tabela a seguir:
Reorganizando a fila de acordo com os critérios descritos anteriormente, mudarão de posição em relação à fila descrita na tabela apenas
(A) A e B. (B) A e C. (C) B e D. (D) B e E (E) C e D.
RESOLUÇÃO:
Observe que A e E são grávidas, tendo prioridade. Delas, A tem prioridade em relação a E, por ser mais velha. Logo, a primeira pessoa deve ser A, e a segunda deve ser E. Dentre as pessoas restantes, como nenhuma é grávida ou tem criança de colo, prevalece a maior idade de C. As pessoas B e D tem a mesma idade, prevalecendo D, por ser mulher. A pessoa B é a última. Ficamos com a ordem:
A – E – C – D – B
As pessoas que mudaram de posição foram B e E.
Resposta: D
ANALISTA JUDICIÁRIO – PROVA DE RACIOCÍNIO LÓGICO RESOLVIDA (AJAJ E OFICIAL)
FCC – TRT/PE – 2018) Um Analista Judiciário precisa distribuir certo número de tarefas por 17 funcionários. Distribuindo-se 13 tarefas por funcionário irão sobrar 4 tarefas sem serem distribuídas entre os funcionários. Se a mesma quantidade de tarefas fosse distribuída igualmente por 24 funcionários, cada funcionário receberia 9 tarefas e sobrariam, sem serem distribuídas entre os funcionários, um total de tarefas igual a
(A) 3.
(B) 7.
(C) 9
(D) 6.
(E) 8.
RESOLUÇÃO:
Devemos lembrar que Dividendo = Divisor x Quociente + Resto. Se dividirmos as tarefas pelo divisor 17 funcionários, temos resultado 13 e resto 4, ou seja,
Tarefas = 17 x 13 + 4 = 225
Se dividirmos essas 225 tarefas por 24 funcionários, teremos resultado 9 tarefas por funcionário, e resto igual a 9 tarefas. Este é o gabarito.
Resposta: C
FCC – TRT/PE – 2018) Quatro quintos dos processos de uma comarca são da área civil e três oitavos desses processos são da regional sul da comarca. A porcentagem de processos da comarca que são da área civil e da regional sul é igual a
(A) 42%.
(B) 20%.
(C) 45%.
(D) 12%.
(E) 30%
RESOLUÇÃO:
Sendo P processos, sabemos que 4/5 são da área civil, ou seja, 4P/5 são dessa área. Destes, 3/8 são da regional sul, ou seja,
área civil e regional sul = (3/8) x 4P/5 = 12P/40 = 3P/10 = 0,3P = 30%.P
Ou seja, 30% dos processos são da área civil e regional sul.
Resposta: E
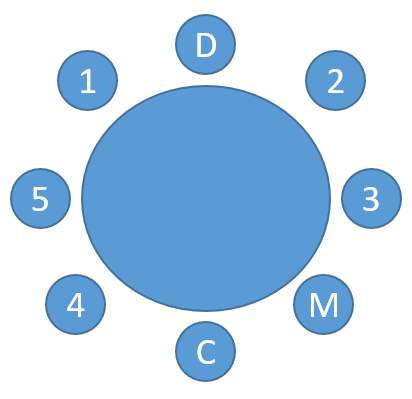
FCC – TRT/PE – 2018) Cinco diretores (Recursos Humanos-RH, Financeiro-F, Administrativo-D, Contábil-C e Marketing-M) estão sentados em uma mesa circular com oito assentos igualmente espaçados ao redor da mesa. D está sentado no assento em frente ao assento de C e no terceiro assento à direita de M. RH está sentado a quatro assentos de F. Em tais condições é correto afirmar que, necessariamente,
(A) M está sentado em frente a um assento vazio
(B) M está sentado ao lado de um assento vazio.
(C) há dois assentos vazios que estão juntos.
(D) D está sentado ao lado de um assento vazio à sua direita e de um à sua esquerda.
(E) C está sentado imediatamente à direita de RH.
RESOLUÇÃO:
Podemos desenhar uma mesa com 8 lugares e posicionar a pessoa D. Veja que C deve estar à sua frente, ou seja, na posição oposta. E M deve estar 3 posições à esquerda de D (para que D esteja 3 posições à direita de M. Ficamos com:
Veja que eu já numerei as posições restantes, para facilitar a explicação. Veja que as pessoas RH e F devem estar frente a frente, pois estão a 4 posições uma da outra. Logo, elas podem ocupar as posições 2 e 4, ou então 3 e 5. Em qualquer caso, a posição 1 permanece desocupada. Isto indica que M não tem ninguém à sua frente, o que permite marcar a letra A.
Resposta: A
FCC – TRT/PE – 2018) A relação entre funcionários homens e funcionárias mulheres em uma repartição pública é de 5 para 4, nessa ordem. Após um concurso, foram admitidos 5 novos funcionários homens e 12 novas funcionárias mulheres nessa repartição. Com o ingresso desses funcionários, a proporção entre funcionários homens e funcionárias mulheres da repartição passou a ser de 9 para 8, nessa ordem. Sendo assim, depois do concurso a repartição passou a ter um total de funcionárias mulheres igual a
(A) 64.
(B) 78.
(C) 80
(D) 72.
(E) 70.
RESOLUÇÃO:
Sendo H e M os homens e mulheres no início, temos:
H/M = 5/4
H = 5M/4
Após entrarem 5 homens e 12 mulheres, ficamos com H+5 homens e M+12 mulheres, e a razão passou para 9/8. Ou seja,
(H+5)/(M+12) = 9/8
8H + 40 = 9M + 108
8.(5M/4) + 40 = 9M + 108
10M + 40 = 9M + 108
10M – 9M = 108 – 40
M = 68
Originalmente havia 68 mulheres. Com as 12 contratações, passamos para 80 mulheres.
Resposta: C
FCC – TRT/PE – 2018) Em uma empresa com 120 funcionários, 42 recebem vale-transporte e 95 recebem vale-refeição. Sabendo que todos os funcionários da empresa recebem ao menos um desses dois benefícios, o total de funcionários que recebem ambos os benefícios é igual a
(A) 25.
(B) 17
(C) 15.
(D) 19.
(E) 20.
RESOLUÇÃO:
Podemos resolver essa questão usando o macete para problemas com 2 conjuntos em que é solicitada a interseção. Basta somar as quantidades de elementos dos dois conjuntos (42 + 95 = 137) e subtrair o total (120), ficando com 137 – 120 = 17 pessoas na interseção, ou seja, pessoas que recebem os dois benefícios.
Resposta: B
FCC – TRT/PE – 2018) Uma equipe de 25 trabalhadores foi contratada para realizar uma obra em 14 dias. Passados 9 dias, a equipe só havia realizado 3/7 da obra. O coordenador da obra decidiu que irá contratar mais trabalhadores, com o mesmo ritmo de trabalho dos 25 que já estão na obra, para dar conta de terminá-la exatamente no prazo contratado. Sendo assim, o coordenador deve contratar um número mínimo de trabalhadores igual a
(A) 36.
(B) 28.
(C) 32.
(D) 42.
(E) 35
RESOLUÇÃO:
Veja que 25 trabalhadores fizeram 3/7 do trabalho em 9 dias. Queremos saber quantos trabalhadores (T) são necessários para fazer os 4/7 restantes do trabalho no prazo restante de 14 – 9 = 5 dias. Ou seja, temos a proporção:
Trabalhadores Dias Obra
25 9 3/7
T 5 4/7
Quanto MAIS trabalhadores, conseguimos fazer MAIS obras em MENOS dias. Devemos inverter a coluna dos dias, ficando com:
Trabalhadores Dias Obra
25 5 3/7
T 9 4/7
Montando a proporção:
25/T = (5/9) x (3/4)
5/T = (1/9) x (3/4)
5/T = (1/3) x (1/4)
5/T = 1/12
5.12 = T.1
60 trabalhadores = T
Como já temos 25 trabalhadores, falta contratar 60 – 25 = 35.
Resposta: E
ANALISTA JUDICIÁRIO – PROVA DE RACIOCÍNIO LÓGICO RESOLVIDA (AJAA)
FCC – TRT/PE – 2018) O número natural x possui ao todo três divisores positivos distintos. O número natural y possui ao todo três divisores positivos distintos. O produto x . y é um número natural maior que 30 e menor que 40. A soma x + y é igual a
(A) 12.
(B) 14.
(C) 13
(D) 16.
(E) 19.
RESOLUÇÃO:
Números cuja fatoração resulta em algo como n2, em que n é um fator primo, possuem exatamente 3 divisores positivos distintos (o número de divisores é obtido somando 1 unidade ao expoente). Assim, números como 22, 32, 52 etc. possuem exatamente 3 divisores positivos distintos. Como devemos escolher 2 números cuja multiplicação fica entre 30 e 40, podemos pensar em 22 . 32 = 4 . 9 = 36. Ou seja, x = 4 e y = 9, de modo que a soma dos dois é 13.
Resposta: C
FCC – TRT/PE – 2018) Duas pessoas, P e Q, distam uma da outra, em linha reta, x metros. Simultaneamente P e Q caminham, uma em direção à outra, durante 15 minutos. P caminha exatamente ¼ de x e Q caminha exatamente 2/5 de x. Nesse momento, a distância que as separam é y. Nos 15 minutos seguintes, P caminha exatamente 1/3 de y e Q caminha exatamente 1/2 de y. Após esses 30 minutos de caminhada, é correto afirmar que
(A) P e Q estão exatamente no mesmo lugar.
(B) P e Q já se cruzaram e estão separadas por uma distância igual a 13/120 de x.
(C) P e Q ainda não se cruzaram e estão separadas por uma distância igual a 7/120 de x
(D) P e Q já se cruzaram e estão separadas por uma distância igual a 17/120 de x.
(E) P e Q ainda não se cruzaram e estão separadas por uma distância igual a 11/120 de x.
RESOLUÇÃO:
Nos primeiros 15 minutos, P andou x/4 e Q andou 2x/5, de modo que a distância entre eles caiu para:
distância = x – x/4 – 2x/5 = 3x/4 – 2x/5 = 15x/20 – 8x/20 = 7x/20
Essa distância é igual a y, ou seja, y = 7x/20.
Nos próximos 15 minutos, P andou y/3, e Q andou y/2. A distância deles caiu para:
distância = y – y/2 – y/3 = y/2 – y/3 = 3y/6 – 2y/6 = y/6
A distância final é, portanto, y/6 = (7x/20)/6 = 7x/120. Ou seja, temos uma distância de 7/120 de x, e P e Q não se cruzaram ainda.
Resposta: C
FCC – TRT/PE – 2018) Ao comprar um produto de R$ 100,00, foram oferecidos para Clóvis dois planos de pagamento. No primeiro plano, ele pagaria no momento da compra, à vista, e receberia um desconto de 4%. No segundo plano, ele pagaria os R$ 100,00 em duas parcelas de R$ 50,00, sendo a primeira após 30 dias da compra, e a segunda após 60 dias da compra. Clóvis tem ao seu dispor um investimento que rende 3% a cada 30 dias. Clóvis escolheu o plano que mais o favorecia e realizou a compra. Comparando-se os dois planos, é correto concluir que a escolha de Clóvis o favoreceu em, aproximadamente,
(A) R$ 0,35
(B) R$ 1,32.
(C) R$ 0,63.
(D) R$ 1,15.
(E) R$ 0,84.
RESOLUÇÃO:
Pagando a vista, Clóvis tem 4% de desconto, pagando 100 x (1-4%) = 100 x (1 – 0,04) = 100 x 0,96 = 96 reais. Assim, sobram 4 reais. Aplicando este valor, ele ganha 3% no primeiro mês, ficando com 4 x (1+3%) = 4 x 1,03 = 4,12. No segundo mês, ele ganha 3% em relação ao que tinha, ficando com 4,12×1,03 = 4,24 reais.
Se for pagar a prazo, durante o primeiro mês 0s 100 reais vão render 3%, chegando ao montante de 100 x 1,03 = 103 reais. Pagando 50 reais, sobram 103 – 50 = 53 reais. Este valor rende 3% no mês seguinte, chegando a 53×1,03 = 54,59 reais. Pagando 50 reais, sobram 4,59 reais.
A diferença entre o valor economizado em cada caso é de 4,59 – 4,24 = 0,35 reais. Veja que vale a pena pagar a prazo.
Resposta: A
FCC – TRT/PE – 2018) Em uma empresa, no ano de 2005, o total de funcionários era 100, e a razão entre o número de homens e o número de mulheres era 7/3. De 2005 até 2010 nenhum funcionário se desligou da empresa e foram feitas contratações de modo a duplicar o número total de funcionários. Após essas contratações a razão, que era 7/3 , passou a ser 3/2. Desse modo, é correto concluir que a razão entre o número de homens contratados e o número de mulheres contratadas, nesse período, foi
(A) 3/4 .
(B) 5/3 .
(C) 2/1 .
(D) 1/1
(E) 4/5 .
RESOLUÇÃO:
No momento inicial temos 70 homens e 30 mulheres, pois desta forma temos um total de 100 pessoas, e a razão entre homens e mulheres é de 70/30 = 7/3.
Foram contratadas mais 100 pessoas (pois duplicamos o total de funcionários), e a razão entre homens e mulheres passou a ser de 3/2, ou seja, tínhamos 120 homens e 80 mulheres (a razão dá 120/80 = 12/8 = 3/2).
Fica claro que foram contratados 120 – 70 = 50 homens, e 80 – 30 = 50 mulheres. A razão entre as contratações é de 50/50 = 1/1.
Resposta: D
FCC – TRT/PE – 2018) Na sequência de números (x, x-1/3, x-2/3, x-3/3, …) a diferença entre o quinto e o nono termos, nesta ordem, é igual a
(A) 5/3 .
(B) 2/3 .
(C) 1.
(D) 7/3 .
(E) 4/3
RESOLUÇÃO:
Continuando o preenchimento da sequência, você verá que o quinto termo é x – 4/3, e o nono termo é x – 8/3. A diferença entre eles, nesta ordem, é:
x – 4/3 – (x – 8/3) = -4/3 + 8/3 = 4/3.
Resposta: E
FCC – TRT/PE – 2018) Considere a afirmação I como sendo FALSA e as outras três afirmações como sendo VERDADEIRAS.
I. Lucas é médico ou Marina não é enfermeira.
II. Se Arnaldo é advogado, então Lucas não é médico.
III. Ou Otávio é engenheiro, ou Marina é enfermeira, mas não ambos.
IV. Lucas é médico ou Paulo é arquiteto.
A partir dessas informações, é correto afirmar que
(A) Paulo não é arquiteto ou Marina não é enfermeira.
(B) Marina é enfermeira e Arnaldo não é advogado.
(C) Se Lucas não é médico, então Otávio é engenheiro.
(D) Otávio é engenheiro e Paulo não é arquiteto.
(E) Arnaldo é advogado ou Paulo é arquiteto
RESOLUÇÃO:
Como a primeira frase é falsa, então as 2 informações nela contidas são falsas (pois esta é uma disjunção simples). Logo,
- Lucas NÃO é médico
- Marina É enfermeira
Com isso, a frase II já fica verdadeira, independentemente de Arnaldo ser advogado ou não, pois a segunda parte da condicional é V. Nada podemos concluir sobre Arnaldo.
Na frase III, como “Marina é enfermeira” é V, então o trecho “Otávio é engenheiro” deve ser F, pois esta é uma disjunção exclusiva. Portanto, Otávio NÃO é engenheiro.
Na frase IV, como a primeira parte é F, a segunda deve ser V para deixar a disjunção simples verdadeira. Portanto, Paulo é arquiteto.
Com as conclusões sublinhadas, podemos julgar as alternativas:
(A) Paulo não é arquiteto ou Marina não é enfermeira.
Aqui temos uma disjunção “F ou F”, que é falsa.
(B) Marina é enfermeira e Arnaldo não é advogado.
Aqui temos uma conjunção “V e ?”, onde a interrogação significa que não sabemos o valor lógico referente a Arnaldo. Não podemos marcar esta letra pois, se por acaso Arnaldo for advogado, a frase fica falsa.
(C) Se Lucas não é médico, então Otávio é engenheiro.
Aqui temos uma condicional do tipo V–>F, que é falsa.
(D) Otávio é engenheiro e Paulo não é arquiteto.
Aqui temos uma conjunção do tipo “F e F”, que é falsa.
(E) Arnaldo é advogado ou Paulo é arquiteto
Aqui temos uma disjunção simples do tipo “? ou V”, que é verdadeira. Não precisamos saber o valor da interrogação, pois basta que uma informação seja verdadeira para que a disjunção simples assuma este valor lógico.
Resposta: E
Saudações.