Categorias: Concursos Públicos

Prova de matemática resolvida – concurso de Oficial dos Bombeiros/RN

Olá pessoal! Seguem abaixo várias questões da prova de matemática de Oficial dos Bombeiros/RN. À medida que eu for terminando as outras questões vou postando aqui. Creio haver chance de recurso naquelas que marquei o gabarito com a observação de que deveria ser anulada. Abraço!

IDECAN – Bombeiros/RN – 2017) A equação da circunferência de centro C = (–2, 3) e que é tangente à reta 21x – 20y –101 = 0 é:

A) (x – 2)² + (y + 3)² = 7.

B) (x + 2)² + (y – 3)² = 7.

C) (x – 2)² + (y + 3)² = 49.

D) (x + 2)² + (y – 3)² = 49.

RESOLUÇÃO:

Se a circunferência é tangente à reta dada, então a distância entre o centro e a reta é igual ao raio. Assim:

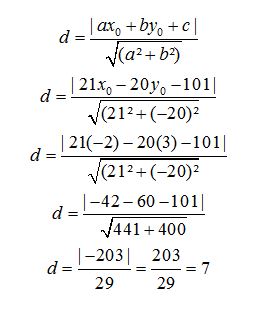
Portanto, a circunferência tem centro em (–2, 3) e raio igual a 7. Sua equação fica sendo:

(x + 2)² + (y – 3)² = 49

Resposta: D

IDECAN – Bombeiros/RN – 2017) Analise as afirmativas a seguir.

I. Se um trapézio tem um ângulo externo reto, ele é trapézio retângulo.

II. Toda propriedade do paralelogramo vale para o losango.

III. Um ângulo agudo e um ângulo obtuso de um paralelogramo são suplementares.

IV. O quadrado tem as propriedades do paralelogramo, do retângulo e do losango.

V. Dois ângulos consecutivos de um paralelogramo sempre são congruentes.

VI. Se as diagonais de um paralelogramo são perpendiculares entre si e se cruzam em seu ponto médio, então esse paralelogramo não é um losango.

Estão INCORRETAS apenas as afirmativas

A) I e VI.
B) V e VI.
C) I, II e III.
D) II, IV e V.

RESOLUÇÃO:

I. Se um trapézio tem um ângulo externo reto, ele é trapézio retângulo.

Incorreto. O trapézio retângulo apresenta dois ângulos retos.

II. Toda propriedade do paralelogramo vale para o losango.

Correto. Losango é um tipo de paralelogramo em que os lados são congruentes.

III. Um ângulo agudo e um ângulo obtuso de um paralelogramo são suplementares.

Correto.

IV. O quadrado tem as propriedades do paralelogramo, do retângulo e do losango.

Correto. Podemos considerar o quadrado como um caso especial de paralelogramo, de retângulo ou mesmo de losango.

V. Dois ângulos consecutivos de um paralelogramo sempre são congruentes.

Incorreto. São suplementares.

VI.Se as diagonais de um paralelogramo são perpendiculares entre si e se cruzam em seu ponto médio, então esse paralelogramo não é um losango.

Incorreto. Em um losango as diagonais são perpendiculares entre si e se cruzam em seu ponto médio.

Resposta: B (mas deve ser anulada, visto que o item I está incorreto)

IDECAN – Bombeiros/RN – 2017) Considerando o polinômio p(y) = – 4y³ + ay² + by – 18 onde 3 é raiz de p(y) e p(–1) = – 20, os valores de a e b são, respectivamente:

A) 8 e 15.

B) 15 e 8.

C) 9 e 15.

D) 15 e 9.

RESOLUÇÃO:

Se 3 é raiz, então p(3) = 0. Assim:

p(y) = – 4y³ + ay² + by – 18

p(3) = – 4 . 3³ + a . 3² + b . 3 – 18 = 0

– 108 + 9a+ 3b – 18 = 0

9a+ 3b = 126

3a+ b = 42

Se p(–1) = – 20, então:

p(y) = – 4y³ + ay² + by – 18

p(-1) = – 4(-1)³ + a(-1)² + b(-1) – 18 = -20

4 + a – b – 18 = -20

a – b = -6

a = b – 6

Substituindo essa informação em 3a+ b = 42, temos:

3(b – 6) + b = 42

3b – 18 + b = 42

4b = 60

b = 15

a = b – 6

a = 15 – 6

a = 9

Resposta: C

IDECAN – Bombeiros/RN – 2017) Considerando o lado “a” o maior lado de um triângulo de lados a, b, c, podemos conhecer a natureza desse triângulo, com bases nas equivalências seguintes; analise-as.

I. a² < b² + c² (triângulo obtusângulo).

II. a² = b² + c² (triângulo retângulo).

III. a² > b² + c² (triângulo acutângulo).

Mediante as equivalências propostas, está(ão) correta(s) apenas

A) I.

B) II.

C) I e II.

D) II e III.

RESOLUÇÃO:

No triângulo obtusângulo, temos um ângulo interno maior que 90º, oposto ao maior lado “a” do triângulo. Dessa forma, para esse tipo de triângulo teremos a² > b² + c².

No triângulo acutângulo, temos todos os ângulos internos menores que 90º. Dessa forma, para esse tipo de triângulo teremos a² < b² + c².

Já para o triângulo retângulo, a afirmação II traz justamente o teorema de Pitágoras, o qual sabemos ser verdadeiro.

Resposta: B

IDECAN – Bombeiros/RN – 2017) A solução do sistema de equações a seguir tem como par ordenado:

x² + 2y² = 54

x – y = -9

A) {(6, 3)}.

B) {(–6, 3)}.

C) {(6, –3)}.

D) {(–6, –3)}.

RESOLUÇÃO:

Nesse tipo de questão é mais fácil testar as alternativas de resposta, tendo em vista que elas são bem semelhantes. Vamos começar testando x = 6. Nesse caso, a segunda equação nos daria:

6 – y = -9

6 + 9 = y

y = 15

Jogando os valores x = 6 e y = 15 na primeira equação, encontramos:

x² + 2y² =

6² + 2 . 15² =

36 + 450 = 486

Veja que encontramos um valor 486 bem diferente daquele que a primeira equação deveria dar, que seria 54. Assim, nossa hipótese de que x = 6 é falsa.

Vamos supor agora que x = -6. Nesse caso, a segunda equação nos daria:

-6 – y = -9

6 + y = 9

y = 3

Jogando os valores x = -6 e y = 3 na primeira equação, encontramos:

x² + 2y² =

(-6)² + 2 . 3² =

36 + 2 . 9 = 36 + 18 = 54

Portanto, a solução do sistema é {(–6, 3)}.

Resposta: B

IDECAN – Bombeiros/RN – 2017) O sistema linear a seguir pode ser classificado considerando o número de soluções como:

x + 2y + z = 0

2x + y – 3z = 8

3x + 3y – 2z = 0

A) Impossível.

B) Possível e determinado.

C) Possível e indeterminado.

D) Admite apenas a solução (1, 3, –4).

RESOLUÇÃO:

Calculando D, temos:

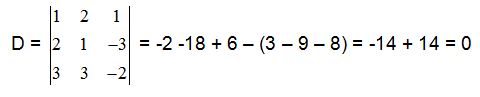
Como D = 0, temos um sistema impossível.

Resposta: A

IDECAN – Bombeiros/RN – 2017) No plano cartesiano, tem-se um triângulo de vértices A(–2, 2), B(12, 6) e C(4, 6). Considerando os dados mencionados, analise as afirmativas a seguir.

I. O triângulo é isósceles.

II. O triângulo é escaleno.

III. O ponto D(2, 3/2) pertence ao segmento AB.

IV. A equação da reta que passa pelos pontos B e C é y – 6 = 0.

Está(ão) correta(s) apenas a(s) afirmativa(s)

A) I.
B) III.
C) IV.
D) II e IV.

RESOLUÇÃO:

Vamos calcular a distância entre os pontos para saber o comprimento de cada lado do triângulo:

Como os três lados são diferentes, o triângulo é isósceles, o que torna a afirmação I falsa e a II verdadeira.

A equação da reta que passa por A e B é dada por:

(yb – ya) = m (xb – xa)

(6 – 2) = m (12 – (-2))

4 = 14 m

m = 4/14 = 2/7

Assim, temos a reta y = (2/7) x + n. Sabendo que a reta passa pelo ponto A, temos:

2 = (2/7) (-2) + n

n = 2 + 4/7

n = 18/7

A equação da reta que passa por A e B é dada por:

y = (2/7) x + 18/7

Para saber se o ponto (2, 3/2) pertence a essa reta, basta fazer x = 2 nela:

y = (2/7) x + 18/7

y = (2/7) 2 + 18/7

y = 4/7 + 18/7

y = 22/7

Como não encontramos y = 3/2 quando fizemos x = 2, temos que o ponto (2, 3/2) não pertence a essa reta, o que torna a afirmação III falsa.

Perceba agora que B e C possuem o mesmo valor de ordenada. Em ambos o valor de y = 6. Portanto, podemos dizer que a reta que passa pelos dois é y = 6, ou seja, y – 6 = 0, o que torna a afirmação IV verdadeira.

Resposta: D

IDECAN – Bombeiros/RN – 2017) A goiabada é uma deliciosa sobremesa típica dos territórios de língua portuguesa, que tem suas origens no período colonial no Brasil, quando a fruta goiaba, usada na preparação de bolo, substitui o marmelo para fazer compotas. No Brasil, a goiabada é consumida geralmente com queijo Minas levando o poético nome de Romeu e Julieta, e é ideal para um delicioso café da manhã em fatias de pão torrado ou servido com queijo fresco. “Dona Aurora foi a Minas e trouxe bastantes barras de goiabada para distribuir com suas três irmãs.” À primeira, a mais velha, ela deu a metade das barras de goiabada mais meia barra de goiabada. À segunda, ela deu 3/4 do que restou e mais meia barra de goiabada. Por último, à terceira, a mais nova, ela deu 5/6 e mais meia barra de goiabada, não sobrando nenhuma com ela. Y representa a quantidade recebida pela segunda irmã. Em relação ao total de goiabadas distribuídas por dona Aurora, a porcentagem que representa a quantidade recebida pela segunda irmã está entre:

A) 30% < y < 60%.

B) 50% < y < 80%.

C) 70% < y < 110%.

D) 90% < y < 120%.

RESOLUÇÃO:

Seja X a quantidade de barras de goiabada que Dona Aurora trouxe de Minas. À primeira irmã, a mais velha, ela deu a metade das barras de goiabada mais meia barra de goiabada, ou seja, X/2 + 1/2. Após isso, restaram:

X – (X/2 + 1/2) = X – X/2 – 1/2 = X/2 – 1/2

À segunda, ela deu 3/4 do que restou e mais meia barra de goiabada, ou seja:

3/4 (X/2 – 1/2) + 1/2=

3X/8 – 3/8 + 1/2 =

3X/8 – 3/8 + 4/8 =

3X/8 + 1/8

Como Y representa a quantidade recebida pela segunda irmã, temos que Y = 3X/8 + 1/8. Assim, restou, para a terceira irmã, X/2 – 1/2 (que é o que tinha sobrado após a primeira irmã receber sua parte) subtraído de 3X/8 + 1/8 (que foi o que a segunda irmã recebeu). Portanto, restou:

X/2 – 1/2 – (3X/8 + 1/8) =

X/2 – 1/2 – 3X/8 – 1/8 =

4X/8 – 4/8 – 3X/8 – 1/8 =

X/8 – 3/8

Por último, à terceira, a mais nova, ela deu 5/6 e mais meia barra de goiabada, ou seja, 5/6 + 1/2 = 5/6 + 3/6 = 8/6. Como após dar a parte da terceira não sobrou nada, o resto que calculamos anteriormente deve ser igual à parte da terceira irmã:

X/8 – 3/8 = 8/6

O MMC entre 8 e 6 é 24. Portanto:

3X/24 – 9/24 = 32/24

3X – 9 = 32

3X = 32 + 9

3X = 41

X = 41/3

A parte que coube para a irmã do meio é Y = 3X/8 + 1/8. Isso, em relação ao total, nos dá o percentual de goiabada recebido pela irmã do meio, que é dado por:

Y/X = (3X/8 + 1/8)/X

Y/X = 3/8 + 1/8X

Y/X = 3/8 + 1/(8 . 41/3)

Y/X = 3/8 + 3/(8 . 41)

Y/X = (3 . 41)/(8 . 41)+ 3/(8 . 41)

Y/X = (123)/(8 . 41)+ 3/(8 . 41)

Y/X = (126)/(8 . 41)

Y/X = 38,4%

Resposta: A

IDECAN – Bombeiros/RN – 2017) A figura a seguir refere-se a três sólidos com raio = 1/6 de 36 cm; a altura do cilindro é 1/2 do raio mais 1 cm e a altura do cone é o dobro da altura do cilindro.

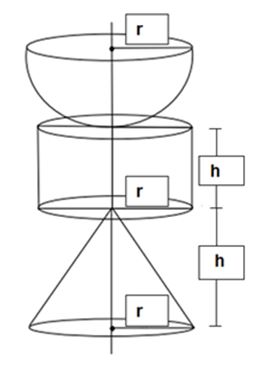
O volume do sólido gerado pela rotação completa em torno do seu eixo é:

A) 240π cm².

B) 240π cm³.

C) 384π cm².

D) 384π cm³.

RESOLUÇÃO:

O volume total será dado pela soma do volume do cone, do cilindro e da meia circunferência. Vamos calcular cada um separadamente e depois somá-los.

Cilindro

raio = r = 1/6 de 36 cm = 6 cm

área da base = Ab = π r² = π 6² = 36π

a altura do cilindro é 1/2 do raio mais 1 cm = h = 1/2 x 6 + 1 = 3 + 1 = 4

volume cilindro = Ab x h = 36π x 4 = 144π