Prova de Matemática Oficial PM-SP resolvida

Olá caros alunos e interessados! Eu sou o prof. Hugo Lima e ministro o curso de Matemática para Oficial da PM/SP aqui no Estratégia.

Hoje eu venho aqui para compartilhar com vocês a resolução da última prova de matemática de Oficial PM-SP, que ocorreu em 2016. É um excelente treino para o próximo certame!

Caso você não me conheça, sou Engenheiro Mecânico-Aeronáutico pelo ITA, fui Oficial da Força Aérea por 5 anos, e atualmente sou Auditor-Fiscal da Receita Federal.

Vamos lá?!

VUNESP – OFICIAL PM/SP – 2016) Para uma atividade curricular, os alunos de certo curso foram divididos em três grupos que, na avaliação do desempenho, receberam, respectivamente, x, y e z pontos. Considere x, y e z três números inteiros distintos, tais que x + y = 50, x + z = 40 e y + z = 42. Considerando-se os três grupos, é correto afirmar que a diferença entre o maior e o menor número de pontos obtidos nessa atividade foi igual a

(A) 8.

(B) 9.

(C) 10.

(D) 12.

(E) 16.

RESOLUÇÃO:

Temos três equações e três incógnitas. Assim:

x + y = 50

y = 50 – x

x + z = 40

z = 40 – x

y + z = 42

(50 – x) + (40 – x) = 42

90 – 2x = 42

2x = 90 – 42

2x = 48

x = 24

y = 50 – x = 50 – 24 = 26

z = 40 – x = 40 – 24 = 16

 

A diferença entre o maior e o menor número de pontos obtidos nessa atividade foi igual a 26 – 16 = 10.

RESPOSTA: C

 

VUNESP – OFICIAL PM/SP – 2016) Uma empresa vende produtos das linhas P e Q. No final de 2015, essa empresa elaborou previsões para as receitas mensais de ambas as linhas, para os 15 meses subsequentes. Para a linha P, foi prevista receita de 240 mil reais em janeiro/2016, com aumentos sucessivos de 15 mil reais a cada mês subsequente. Para a linha Q, foi prevista receita de 120 mil reais em janeiro/2016, com aumentos sucessivos de 25 mil reais a cada mês subsequente. Nessas condições, a receita mensal prevista para a linha P será exatamente igual à receita mensal prevista para a linha Q no mês de

(A) setembro/2016.

(B) novembro/2016.

(C) dezembro/2016.

(D) janeiro/2017.

(E) fevereiro/2017

RESOLUÇÃO:

         Seja P(x) a receita prevista pra a linha P, em função do mês x. Sabemos que quando x = 1, ou seja, em janeiro, a função P(x) vale 240 mil. Além disso, a cada mês temos um incremento de 15 mil reais. Logo, a função P(x) é dada por:

P(x) = 15.000x + 225.000

        Seja Q(x) a receita prevista pra a linha Q, em função do mês x. Sabemos que quando x = 1, ou seja, em janeiro, a função Q(x) vale 120 mil. Além disso, a cada mês temos um incremento de 25 mil reais. Logo, a função Q(x) é dada por:

Q(x) = 25.000x + 95.000

        Nessas condições, a receita mensal prevista para a linha P será exatamente igual à receita mensal prevista para a linha Q quando:

P(x) = Q(x)

15.000x + 225.000 = 25.000x + 95.000

10.000x = 130.000

x = 13

 

        Como x = 1 corresponde a janeiro de 2016, x = 12 corresponde a dezembro de 2016 e, assim, x = 13 corresponde a janeiro de 2017.

RESPOSTA: D

 

VUNESP – OFICIAL PM/SP – 2016) Um terreno, com a forma de um triângulo ABC, foi dividido em duas regiões pelo segmento ED, conforme mostra a figura.

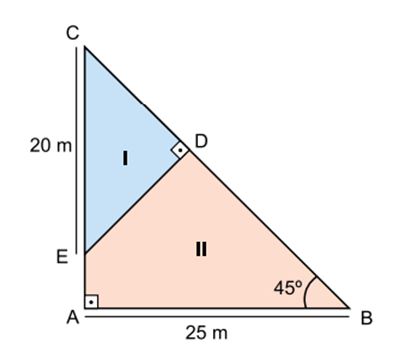
A área da região delimitada pelo quadrilátero ABDE é, em m², igual a

(A) 215,5.

(B) 212,5.

(C) 205.

(D) 162,5.

(E) 142.

RESOLUÇÃO:

         A área de ABDE nada mais é que a diferença entre a área do triângulo ABC e a área do triângulo CDE. Assim, temos:

Área_ABDE = Área_ABC – Área_CDE

Área_ABDE = (base_ABC x altura_ABC)/2 – (base_CDE x altura_CDE)/2

        Tanto ABC quando CDE são triângulos retângulos cujos outros ângulos são de 45º. Isso nos diz que a base é igual a altura em cada um desses dois triângulos.

        Na figura, vemos que a base do triângulo ABC é 25 m. Portanto, sua altura deve ser de 25 m também.

        Na figura, vemos que 20 m é a medida da hipotenusa do triângulo CDE. Seja L o comprimento de cada cateto desse triângulo. Assim, por Pitágoras, temos:

L² + L² = 20²

2L² = 400

L² = 200

L = √200 = 10√2

        Voltando à nossa fórmula inicial, temos:

Área_ABDE = (base_ABC x altura_ABC)/2 – (base_CDE x altura_CDE)/2

Área_ABDE = (25 x 25)/2  – (10√2 x 10√2)/2

Área_ABDE = 625/2  – 200/2

Área_ABDE = 425/2

Área_ABDE = 212,5 m²

RESPOSTA: B

 

VUNESP – OFICIAL PM/SP – 2016) Na Academia da Polícia Militar, dois alunos do 4º ano e três alunos do 1º ano disputam uma competição de tiro ao alvo. Alunos do mesmo ano são igualmente hábeis, mas sabe-se que, historicamente, a probabilidade de um aluno do 4º ano ganhar é o dobro da probabilidade de um aluno do 1º ano ganhar. Nessas condições, a probabilidade de que um aluno do 1º ano ganhe essa competição é

(A) 4/9

(B) 3/7

(C) 1/3

(D) 1/5

(E) 1/16

RESOLUÇÃO:

        Seja p a probabilidade de um aluno do 1º ano ganhar a competição. Assim, como a probabilidade de um aluno do 4º ano ganhar é o dobro da probabilidade de um aluno do 1º ano ganhar, a probabilidade de um aluno do 4º ano ganhar é 2p.

        Ao todo temos dois alunos do 4º ano e três alunos do 1º ano, ou seja, somente algum deles pode ganhar a competição. Isso significa que se somarmos as probabilidades de cada um deles ganhar a competição, devemos obter 100%. Assim:

2p + 2p + p + p + p = 100%

7p = 1

p = 1/7

        Assim, individualmente, cada aluno do 1º ano tem uma chance de 1/7 de ganhar a competição. Como temos três alunos do 1º ano, as chances sobem para 3 x (1/7) = 3/7.

RESPOSTA: B

 

VUNESP – OFICIAL PM/SP – 2016) Em uma circunferência de raio igual a 5 cm, c₁ é o comprimento do arco de π/6 radianos e c₂ é o comprimento da corda AB determinada por este arco, conforme mostra a figura.

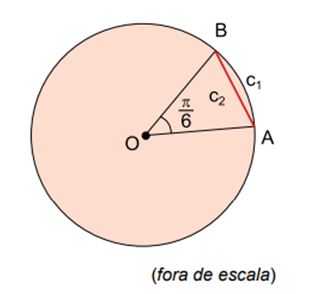
Nessas condições, é correto afirmar que AB mede, em centímetros,

 

 

 

 

 

 

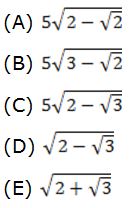
RESOLUÇÃO:

        Temos um triângulo do qual conhecemos dois lados (que coincidem com o raio da circunferência) e o ângulo entre eles. Queremos descobrir o comprimento do terceiro lado desse triângulo. Basta aplicar a lei dos cossenos:

a² = b² + c² – 2.b.c.cosA

        No nosso caso, o lado que queremos é “a”, correspondente a c₂. Os lados “b” e “c” já são por nós conhecidos e valem 5 cm. Já o ângulo “A” corresponde a π/6. Assim, temos:

c₂² = 5² + 5² – 2 . 5 . 5 . cos(π/6)

c₂² = 25 + 25 – 50cos(π/6)

c₂² = 50 – 50cos(π/6)

        π/6 corresponde ao ângulo 30º, cujo cosseno é igual a √3/2. Assim:

c₂² = 50 – 50(√3/2)

c₂² = 50(1 – √3/2)

c₂² = 50(2 – √3)/2

c₂² = 25(2 – √3)

c₂ = √(25(2 – √3))

c₂ = 5√(2 – √3)

RESPOSTA: C

        

VUNESP – OFICIAL PM/SP – 2016) Em um sistema de coordenadas cartesianas ortogonais, y’ é a equação da parábola gerada quando a curva y = x² – 2x + 3 é refletida pelo eixo x. Ligando-se os vértices das parábolas e o ponto O (origem do sistema), obtém-se um triângulo PQO, de área igual, em u.a. (unidade de área), a

(A) 8.

(B) 6.

(C) 5.

(D) 4.

(E) 2.

RESOLUÇÃO:

        Calculando o vértice da parábola dada no enunciado, temos:

X_vértice = -b/2a

X_vértice = -(-2)/2

X_vértice = 1

 

        Substituindo esse valor na parábola dada no enunciado, temos:

y_vértice = x_vértice² – 2x_vértice + 3

y_vértice = 1² – 2 + 3

y_vértice = 1 – 2 + 3 = 2

        O vértice da parábola y está em (1; 2) e ela tem concavidade voltada para cima. Como a parábola y’ é a reflexão da parábola y pelo eixo x (é como se o eixo x fosse um espelho), então o vértice da parábola y’ terá o mesmo valor de X’_vértice = 1, só que o valor da ordenada será o oposto, ou seja, o y’ do vértice será de -2.

        Ficamos com a situação mostrada no gráfico abaixo:

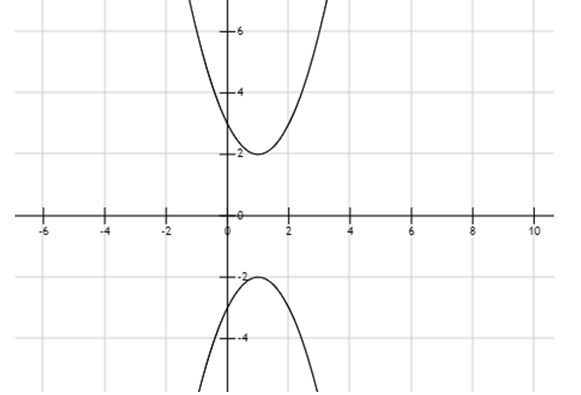
        Ligando-se os vértices das parábolas e o ponto O (origem do sistema), obtém-se um triângulo PQO, em que a base do triângulo mede 4 (visto que vai de 2 até -2) e sua altura mede 1 (valor de x nos vértices). Veja o triângulo abaixo:

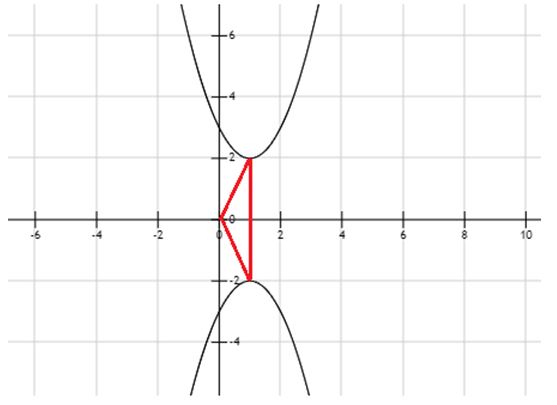
        Portanto, a área do triângulo é (4 x 1)/2 = 4/2 = 2 u.a.

RESPOSTA: E

 

VUNESP – OFICIAL PM/SP – 2016) Para avaliar a aptidão física, fase eliminatória em um concurso, todos os candidatos foram submetidos a uma bateria de 5 testes. Sabe-se que, para cada teste, os dois únicos resultados possíveis eram: reprovado, e, nesse caso, o candidato receberia zero ponto; ou aprovado, e, nesse caso, o candidato receberia 50 pontos, sendo o resultado final dado pela soma dos pontos obtidos nos 5 testes. A tabela mostra a porcentagem de candidatos aprovados em cada um dos cinco testes.

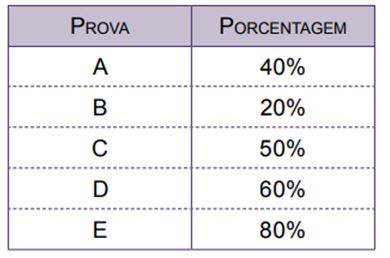
Nessas condições, é correto afirmar que a média aritmética do número de pontos obtidos pelos candidatos nessa avaliação foi igual a

(A) 200.

(B) 175.

(C) 150.

(D) 125.

(E) 100.

RESOLUÇÃO:

         Para facilitar, vamos supor que tenhamos 100 candidatos. Assim, se 40% dos candidatos passaram no teste A, isso significa que 40 candidatos passaram no teste A. Dessa forma, esses 40 candidatos somaram 40 x 50 = 2000 pontos. Seguindo esse raciocínio, podemos construir a tabela abaixo:

Prova	Porcentagem	Candidatos Aprovados	Pontos totais
A	40%	40	2000
B	20%	20	1000
C	50%	50	2500
D	60%	60	3000
E	80%	80	4000

        Portanto, esses 100 candidatos obtiveram juntos 2000 + 1000 + 2500 + 3000 + 4000 = 12.500 pontos. Dividindo pelo total de candidatos (100) obtemos a média de 12500/100 = 125 pontos por candidato.

RESPOSTA: D

 

VUNESP – OFICIAL PM/SP – 2016) Um Grupamento de Operações Especiais trabalha na elucidação de um crime. Para investigações de campo, 6 pistas diferentes devem ser distribuídas entre 2 equipes, de modo que cada equipe receba 3 pistas. O número de formas diferentes de se fazer essa distribuição é

(A) 6.

(B) 10.

(C) 12.

(D) 18.

(E) 20.

RESOLUÇÃO:

         Precisamos dividir as 6 pistas em dois grupos de 3 pistas. Na verdade, basta descobrir o número de formas de escolher 3 pistas em 6, visto que ao escolher 3 pistas, restarão outras 3 pistas que vão compor o outro grupo de pistas.

        Dessa forma, de quantas formas podemos escolher 3 pistas em um grupo de 6? Aqui a ordem não é relevante. Estamos diante de um caso de combinação:

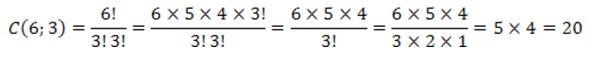
RESPOSTA: E

 

VUNESP – OFICIAL PM/SP – 2016) Em um sistema de coordenadas cartesianas ortogonais, a circunferência de centro O e raio r é definida pela equação:

(x – 4)² + (y – 5)² = 9

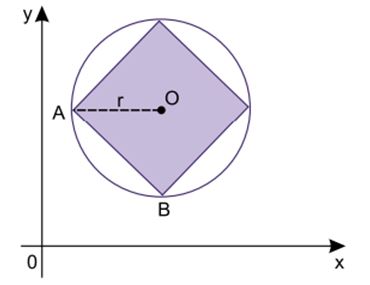
Sendo AB o lado de um quadrado inscrito nessa circunferência,

é correto afirmar que o perímetro desse quadrado mede

(A) 16√2

(B) 14√2

(C) 12√2

(D) 8√2

(E) 6√2

RESOLUÇÃO:

        Temos a equação da circunferência:

(x – 4)² + (y – 5)² = 9

        A partir dessa equação, fica fácil saber se a circunferência tem raio igual a √9 = 3 e centro localizado em (4; 5).

        O raio da circunferência corresponde à metade da diagonal D do quadrado. Logo, dois raios são iguais à diagonal D. Portanto, D = 6.

        Suponha que o quadrado tenha lado L. Assim, sua diagonal em função do lado L é dada por:

        Como o exercício pediu o perímetro do quadrado, basta multiplicar o lado por 4:

4L = 12√2

RESPOSTA: C

 

VUNESP – OFICIAL PM/SP – 2016) Uma empresa está desenvolvendo dois potes, P1 e P2, para comercializar um cosmético. Ambos deverão ter a forma de cilindros circulares retos e volumes iguais. As figuras, com dimensões indicadas em centímetros, mostram as proposições iniciais para cada pote.

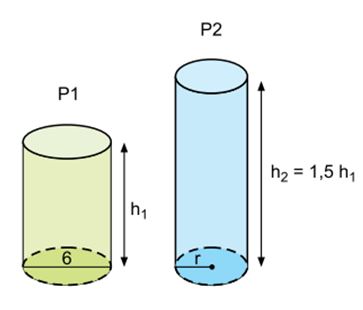
Nessas condições, se a empresa adotar h1 = 10 cm para P1, a medida do raio de P2, em centímetros, deverá ser igual a

(A) √6

(B) 2√3

(C) 2√6

(D) 3√6

(E) 4√3

RESOLUÇÃO:

        O volume do cilindro é dado por área da base (πr²) vezes a altura. Assim, como os dois potes tem volumes iguais, podemos dizer que:

Volume₁ = Volume₂

(Π . r₁²)h₁ = (Π . r₂²)h₂  

r₁² . h₁ = r₂² . 1,5 . h₁

3² . 10 = r₂² . 1,5 . 10  

9 . 10 = r₂² . 15

90/15 = r₂²

r₂² = 6

r₂ = √6

RESPOSTA: A

 

Você sabia que o Estratégia possui um pacote completo para você que está se preparando para o concurso de Oficial da PM-SP? Clique aqui para ter mais informações.

Caso você queira conhecer mais do nosso curso de Matemática para Oficial da PM-SP, clique aqui.