Progressão Aritmética e Progressão Geométrica – Aplicação em concursos
Olá, pessoal, no artigo de hoje trataremos sobre as aplicações de Progressão Aritmética e Progressão Geométrica nas provas de concurso. Vamos lá?
Definição
Progressão nada mais é que o desenvolvimento de uma sequência que segue uma lei de formação (uma fórmula matemática). No nosso cotidiano estamos diante de várias sequências, tais como:
- Aniversários: (20 anos, 21 anos, 22 anos e etc.)
- Anos de copa do mundo: (1994, 1998, 2002 e etc.)
- Sequência dos números naturais: (0, 1, 2, 3, 4 e etc.)
Dentro desse contexto temos a Progressão Aritmética e Progressão Geométrica que exploraremos a seguir.
Progressão aritmética (PA)
A progressão aritmética é uma sequência numérica que corresponde, a partir do segundo termo, à soma do termo anterior com uma constante. Essa constante chamamos de razão (r).
PA (a; a+r; a + 2r; …)
Imaginemos que temos um termo inicial que valha 1 e que a razão seja de 3, teremos a seguinte sequência:
{1; 4; 7; …}
Bem tranquilo, não é mesmo? Mas e se quisermos saber o 99º termo? Seria muito trabalhoso realizar essa sequência “na mão”, por isso a necessidade de conhecermos as fórmulas que exploraremos à frente.
Além disso, a P.A poderá ser classificada como:
- Crescente: (1; 2; 3…) r = +1
- Decrescente: (1; 0; -1) -> r = -1
- Constante: (1; 1; 1) -> r = 0
Obs. A classificação nem é tão importante assim, mas devemos observar que os valores poderão ser positivos ou negativos a depender do caso.
Progressão geométrica (PG)
Já a progressão geométrica é uma sequência numérica que corresponde, a partir do segundo termo, à multiplicação do termo anterior pela razão (q).
PG [a; a.q; a.q²; …]
Vamos utilizar os mesmos números do exemplo anterior para determinar a sequência utilizando a PG.
{1; 3; 9; …}
Referente às classificações, além das que vimos na PA, a PG também poderá ser oscilante, quando a razão (q) for menor que 0.
{1; -2; 4; -8; 16;…}
Fórmulas PA
Agora que já definimos o conceito de PA vejamos as principais fórmulas associadas ao tema.
Definição: Já definimos a PA, mas matematicamente ela pode ser descrita.
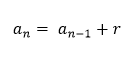
Termo Geral: Trata-se da fórmula mais importante, essa deve ser decorada.
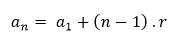
Razão: A razão pode ser definida pela diferença entre dois termos consecutivos.
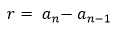
Soma dos termos:
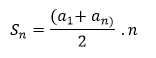
Essa fórmula pode ser bem útil para encontrar a soma dos termos da sequência.
Voltando ao nosso exemplo de PA (a1 = 1 e r = 3), vamos encontrar a soma dos cinco primeiros termos.
Primeiro determinaremos o quinto termo.
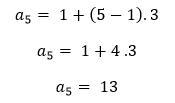
Agora basta aplicar a fórmula
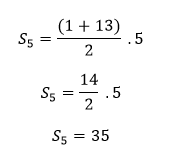
Veja que é muito mais fácil que encontrar toda a sequência e somá-la termo a termo.
∑{ 1; 4; 7; 10; 13} = 35
Equivalência dos termos da PA: Trata-se de uma propriedade interessante da PA, em que:
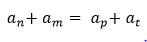
Onde,
n + m = p + t
Utilizando os valores da sequência anteriormente vista {1; 4; 7; 10; 13}, teremos que:
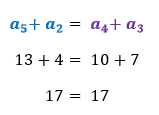
Essa fórmula é bem útil para determinar um termo a partir de outros termos dados pelo exercício, sem conhecer a razão, por exemplo.
Fórmulas PG
As principais fórmulas para a Progressão Geométrica são:
Definição:
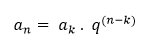
Termo Geral:
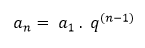
Razão: A razão pode ser encontrada pela divisão entre dois termos consecutivos.
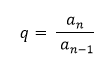
Soma dos termos:
Aqui temos uma diferença em relação à P.A, pois podemos encontrar a soma de “n” termos da mesma forma que a PA, porém também podemos encontrar a soma infinita dos termos, desde que a razão esteja entre -1 e 1.
Soma finita dos termos:
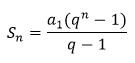
Vamos encontrar a soma dos cinco primeiros termos da PG, considerando que a1 = 1 e r = 3.
O quinto termo será:
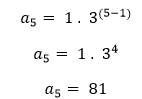
Então,
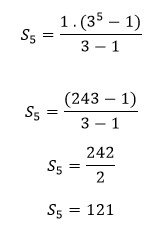
Confirmando,
∑{1; 3; 9;27; 81} = 121
Soma infinita dos termos:
Para somas de infinitos termos utilizamos a seguinte fórmula (atenção à condição!):
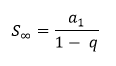
Condição: -1 < q < 1
Exemplo numérico:
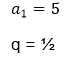
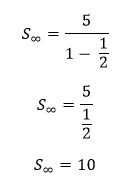
E existe uma explicação? Claro, ao avançarmos na sequência (n tendendo ao infinito) em que a razão (q) atende à condição -1 < q < 1, os valores serão cada vez menores, tendendo a zero, dessa forma é possível determinar o valor da soma, essa é a ideia de limite.
{ 5; 2,5; 1,25; 0,625; 0,3125; 0,15625; 0,078125; ….}
Equivalência dos termos da PG: Assim como na PA, é possível determinar um termo a partir de sua “distância/posição”, porém atenção, pois na PG encontraremos a partir do produto e não da soma.
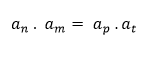
Onde,
n + m = p + t
Utilizando os números de nossa sequência {1; 3; 9; 27; 81} teremos que:
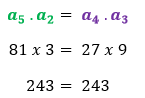
Resumo Estratégico
Com objetivo de facilitar sua revisão, vejamos uma tabela com as fórmulas que resolvem a grande maioria dos exercícios sobre Progressão Aritmética e Progressão Geométrica.

Venda na prática
Agora vamos resolver duas questões de PA e duas de PG para sedimentar o que vimos até aqui.
Exercícios PA
CESPE/2019 – Técnico (TJ PR)
O protocolo de determinado tribunal associa, a cada dia, a ordem de chegada dos processos aos termos de uma progressão aritmética de razão 2: a cada dia, o primeiro processo que chega recebe o número 3, o segundo, o número 5, e assim sucessivamente. Se, em determinado dia, o último processo que chegou ao protocolo recebeu o número 69, então, nesse dia, foram protocolados
a) 23 processos.
b) 33 processos.
c) 34 processos.
d) 66 processos.
e) 67 processos.
Primeiro destacaremos as informações importantes do enunciado:
- r = progressão aritmética de razão 2
- a1 =
o primeiro processo que chega recebe o número 3
- an =
o último processo que chegou ao protocolo recebeu o número 69
Assim,
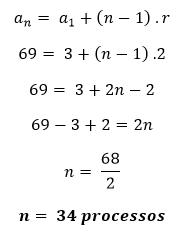
Alternativa C
VUNESP/2020 – Cabo (PMSP)
O percurso de um treinamento de corrida é composto por 5 etapas com distâncias diferentes em cada uma delas. Uma nova etapa sempre tem 100 metros a mais que a etapa anterior. Sabendo que a quarta etapa do treinamento é percorrer 1 200 metros, a distância total do percurso é igual a
a) 6 100 metros.
b) 5 900 metros.
c) 5 700 metros.
d) 5 500 metros.
Novamente vamos separar as informações importantes:
- r = Nova etapa sempre tem 100 metros a mais que a etapa anterior
- a4 = Quarta etapa do treinamento é percorrer 1.200 metros
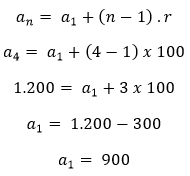
A distância total do percurso é igual a somatória dos termos da PA, logo:
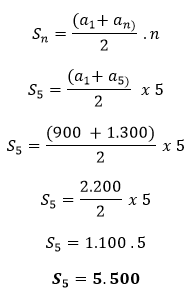
Alternativa D
Exercícios PG
CESPE/2020 – Analista (TJ PA)
No dia 1.º de janeiro de 2019, uma nova secretaria foi criada em certo tribunal, a fim de receber todos os processos a serem protocolados nessa instituição. Durante o mês de janeiro de 2019, 10 processos foram protocolados nessa secretaria; a partir de então, a quantidade mensal de processos protocolados na secretaria durante esse ano formou uma progressão geométrica de razão igual a 2.
Nessa situação hipotética, a quantidade de processos protocolados nessa secretaria durante os meses de junho e julho de 2019 foi igual a
a) 320.
b) 480.
c) 640.
d) 960.
e) 1.270.
Dados da questão:
a1= Durante o mês de janeiro de 2019, 10 processos foram protocolados
- q = progressão geométrica de razão igual a 2
Logo, a quantidade do mês junho de junho será:
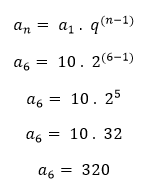
Agora para encontrar o mês de julho basta multiplicar a quantidade de junho pela razão (lembre-se da definição!).
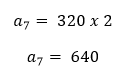
Assim, a quantidade de processos protocolados nessa secretaria durante os meses de junho e julho de 2019 foi igual a
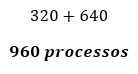
Alternativa D
FCC/2019 – Analista (TRF 3ª)
Um carro percorreu 3.000 km. A cada dia de viagem, a partir do primeiro, ele dobrou a distância percorrida no dia anterior. Se ele finalizou a viagem em quatro dias, a distância percorrida, em quilômetros, no primeiro dia foi de
a) 100.
b) 200.
c) 150.
d) 250.
e) 300.
Para finalizar, uma questão que aborda a soma dos termos de uma PG.
Dados:
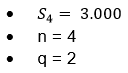
O primeiro ponto a se notar é que a razão não está no intervalo de -1 e 1 e que se trata de uma soma finita de valores, então:
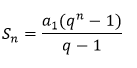
Obs. Atenção, pois a somatória dos termos da PG, como vimos, tem duas fórmulas possíveis, uma para termos infinitos e outra para termos finitos.
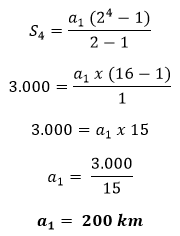
Alternativa B
Considerações Finais
Caso tenha restado alguma dúvida ou queira aprofundar o conhecimento no tema, aconselho o curso básico de matemática nas aulas 22 e 23.
Por hoje é só, espero que o artigo tenha colaborado com seus estudos sobre Progressão Aritmética e Progressão Geométrica.
Até a próxima;
Leonardo Passarin
Instagram: @leonardompassarin
Assinatura Anual Ilimitada*
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
ASSINE AGORA – Assinatura Ilimitada
Fique por dentro de todos os concursos: