Resumo sobre Mediana e Moda para ISS-BH – Estatística

Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo sobre Mediana e Moda para ISS-BH.

Além da mediana e moda, também revisaremos sobre o Box Plot.

Sem mais delongas, vamos lá.

Medidas Separatrizes

Vamos iniciar o Resumo sobre Mediana e Moda para ISS-BH pela Medidas Separatrizes.

Como o nome sugere, são as medidas que separam uma série ordenada em partes.

• Mediana: divide em partes de 50%
• Quartis: divide em partes 25%
• Quintis: divide em partes de 20%
• Decis: divide em partes de 10%
• Percentis: divide em partes de 1%

Vamos focar naquilo que é mais cobrado em concurso, a mediana.

Mediana

A mediana é a posição central de uma série de valores, separando assim a série em duas partes iguais.

Obs.: A mediana é simultaneamente uma medida de posição, de tendência central e separatriz.

Mediana para dados não-agrupados

• Se “n” for ímpar -> faça n/2 e utilizar a próxima posição
• Se “n” for par -> faça n/2 e encontrar a média entre a posição encontrada e a próxima posição

Vamos utilizar um exemplo número para facilitar.

• [1; 2; 3; 5; 7; 8; 9], como n é ímpar temos que:

7/2 = 3,5, logo será o quarto termo, assim mediana será 5

1; 2; 3 – 5 – 7; 8; 9

• [1; 2; 3; 5; 7; 8; 9; 10], como n é par, temos que:

7/2 = 3,5, logo será a média do 4º termo com o 5º termo

5 + 7 / 2 = 6

1; 2; 3; – 5 7 – 8; 9; 10

Obs.: Trata-se de uma conversão adotada, pois o valor da mediana poderia ser qualquer valor entre 5 e 7.

Podemos dizer que:

Mediana para dados agrupados sem intervalos de classe

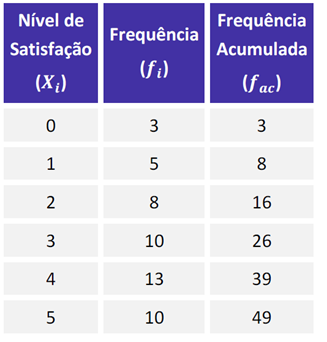
Como a somatória da frequência é 49, assim podemos usar o mesmo raciocínio que vimos

49/2 = 24,5, logo utilizamos a próxima posição (25º)

Logo a mediana será 3, pois X= 3 está entre as posições 17º e 26º

Mediana para dados agrupados em classes

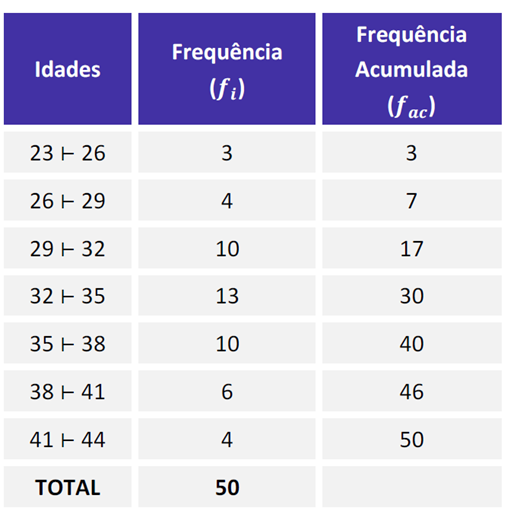
Dividendo a frequência por 2 temos que:

50/2 = 25º

Assim, pela frequência acumulada é possível verificar que a mediana está na quarta classe.

Vamos desenhar a situação

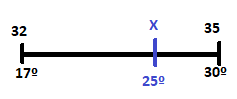
Basta que encontremos essa proporção e assim podemos encontrar a mediana sem a utilização de nenhuma fórmula.

(35 – X) / (30º – 25º) = (35 – 32) / (30º – 17º)

(35 – X) / 5 = 3 / 13

X = 35 – (15/13)

X = 33,85

Propriedades da Mediana

Agora vejamos duas propriedades da mediana.

• 1º Propriedade: Na soma ou a subtração de uma constante k, a mediana do conjunto fica aumentada (ou diminuída) dessa constante.
• 2º Propriedade: Na multiplicação ou divisão por uma constante k, a mediana do conjunto fica multiplicada (ou dividida) por esta constante.

Dando continuidade ao Resumo sobre Mediana e Moda para ISS-BH, vejamos sobre o Box Plot.

O Box Plot (diagrama de caixa) é uma forma gráfica de representação que permite visualizar a distribuição dos dados e os valores discrepantes (outliers).

Vejamos agora uma imagem esquematizada do Box Plot.

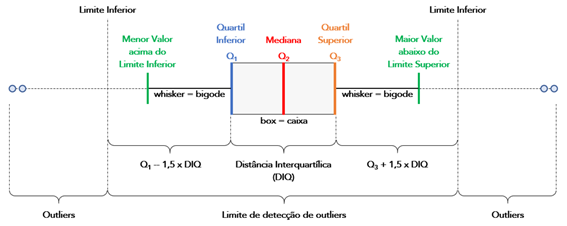
Atente-se que se considera outliers os valores que fogem dos limites em mais de 50% do valor da Distância interquartílica.

Ainda, não confunda:

• Distância interquartílica (amplitude interquartílica):

DIQ = Q3 – Q1

• Desvio quartílico

Dq = (Q3 – Q1) / 2

Moda

Para finalizar o Resumo sobre Mediana e Moda para ISS-BH, vejamos sobre a moda.

A moda descreve o valor de maior ocorrência (frequência) dentre os valores observados.

Atente-se que o conjunto pode possuir uma (unimodal) ou mais modas (bimodal, trimodal ou plurimodal) ou até mesmo nenhuma (amodal).

Exemplo:

Amodal = {1, 2, 3, 5, 6, 8, 10}

Bimodal = {1, 2, 2 ,3, 5, 5, 8} – Mo = 2 e 5

Ainda, a moda também pode ser utilizada para medidas de posição de variáveis qualitativas nominais, atenção!

Moda para dados não-agrupados

Esse aqui é bem tranquilo, basta encontrar o número de maior frequência.

Exemplo: [1, 2, 2, 3, 3, 5, 5, 5, 6, 8, 10]

Nesse caso a moda será igual a 5.

Moda para dados agrupados sem intervalos de classe

Bem tranquilo também, basta encontrar o valor de maior frequência absoluta.

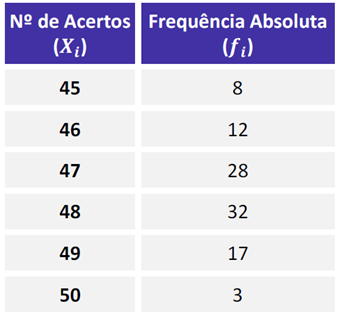
Nesse sentido, temos que a moda é igual a 48, uma vez que é o valor de maior frequência.

Moda para dados agrupados em classes

Existem diversos modos de calcular a moda, como a moda bruta, moda de Pearson e etc., assim aconselhamos a buscar o conteúdo das aulas para aprofundamento do assunto.

Aqui vamos tratar uma forma simples de forma gráfica que costuma atender a grande maioria dos exercícios do tema.

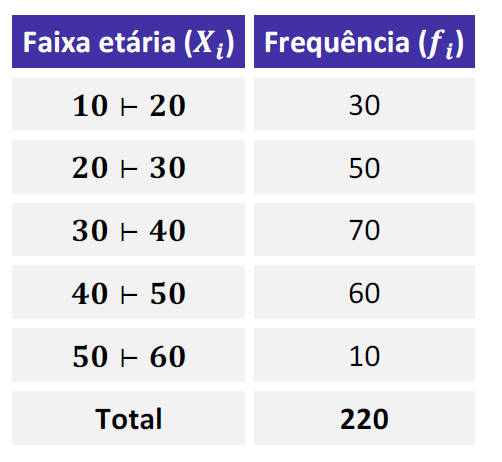
Sabemos que a moda é o valor de maior frequência, logo ela estará entre 30 e 40. Assim graficamente podemos representar da seguinte forma:

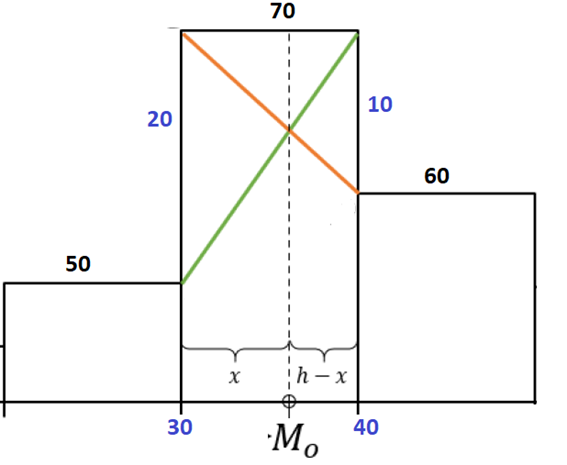
Logo, temos que

(30 – Mo) / 20 = (40 – Mo) / 10

Simplificando

(30 – Mo) / 2 = 40 – Mo

Assim,

30 – Mo = 80 – 2Mo

3Mo = 110

Então,

Mo = 36,67

Propriedades da Moda

Agora vejamos duas propriedades da moda.

• 1ª Propriedade: Na soma ou subtração de uma constante k, a moda do conjunto fica aumentada (ou diminuída) dessa constante.
• 2ª Propriedade: Na multiplicação ou divisão de uma constante k, a moda do conjunto fica multiplicada (ou dividida) por essa constante

Vendo na prática

Apenas para fecharmos o que vimos, vamos verificar um exercício do cálculo de moda e mediana.

CESPE/TCE-RJ/2021 – Considerando que a tabela precedente mostra a distribuição de frequências de uma variável quantitativa X, julgue o item a seguir.

A moda e a mediana da variável X são, respectivamente, iguais a 2 e 1,5.

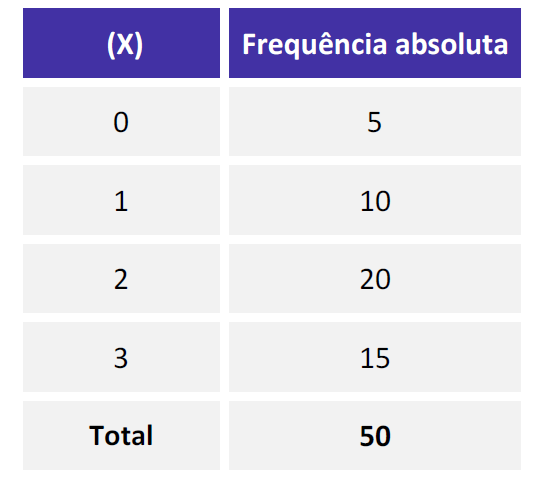
Gabarito: Errado.

Veja, a moda é igual a 2 de fato, pois é a maior frequência, entretanto a mediana não é igual 1,5.

A mediana na realidade é igual a 2 também, pois como n é par o valor da média é igual a média entre a posição 25º e 26º, ambas 2.

Considerações Finais

Pessoal, chegamos ao final do Resumo sobre Resumo sobre Mediana e Moda para ISS-BH. Espero que o artigo tenha sido efetivo para seu aprendizado.

Obviamente trata-se de um resumo apenas com os pontos principais da matéria, assim não deixe de acompanhar as aulas para o aprofundamento necessário.

Ressaltamos mais uma vez a importância de praticar por exercícios, assim faça muitas questões pelo nosso sistema de questões.

Sistema de Questões (SQ) – Estratégia Concursos

Gostou do artigo? Não deixe de seguir

https://www.instagram.com/resumospassarin/

Cursos e Assinaturas

Até mais e bons estudos!