Revise, neste artigo, os principais tópicos de Matemática Financeira para a SEFAZ MG, tais como juros e sistemas de amortização.
Olá, pessoal! O concurso da Secretaria de Fazendo de Minas Gerais (SEFAZ MG) é uma excelente oportunidade para os alunos da área fiscal. Segundo o edital publicado, são 431 vagas para o cargo de Auditor Fiscal, com uma excelente remuneração inicial.
A alteração das datas das provas objetiva e subjetiva proporcionou um precioso tempo a mais para estudar bastante nesse pós-edital.
Neste artigo, trataremos de Matemática Financeira, disciplina presente no Módulo III da parte de Conhecimentos Gerais do edital, para todas as Áreas do Conhecimento.
A seguir, serão destrinchados os principais conceitos, que não são essencialmente complicados. O grande segredo dessa matéria é a resolução de exercícios, que é importante tanto para fixar bem os conceitos quanto para ganhar tempo na prova.
Mãos à obra!
Antes de passar aos conceitos básicos de Matemática Financeira, é importante entender a ideia de que o dinheiro tem valor no tempo, afinal é essa compreensão que dá sentido a todos as fórmulas e cálculos que são feitos. Mas o que isso significa?
Um exemplo deixa essa ideia muito clara: R$ 100,00 hoje não têm o mesmo valor de 5 anos atrás. Ou seja, o dinheiro não pode ser expresso apenas por um número; ele precisa estar associado também a uma data para que uma comparação ou uma avaliação do seu valor possa ser feita.
Dois fatores estão ligados a esse conceito. Primeiramente, a inflação, que representa a variação do nível geral de preços da economia. Devido a essa variação, o dinheiro perde poder de compra com o passar do tempo.
O segundo fator relevante são os juros, que consistem em um prêmio pela espera para o uso de recursos. Se não houvesse juros, seria sempre preferível gastar o dinheiro o mais cedo possível, já que, devido à inflação, o dinheiro perde valor. Assim, os investidores só aceitam deixar de usar seu dinheiro se forem recompensados por isso, recebendo os juros.
Da mesma forma, em operações de crédito, o cliente paga um valor a mais pelo dinheiro recebido em um empréstimo, ou mesmo pelo atraso no pagamento do cartão de crédito.
De modo geral, o valor dos juros será igual ao valor futuro, recebido após algum tempo decorrido, menos o valor presente:
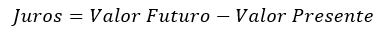
A taxa de juros é simplesmente o valor dos juros dividido pelo valor presente.
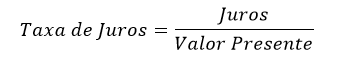
Existem dois Métodos de Capitalização, que dizem respeito ao modo como os juros podem ser calculados quando a taxa de juros incide em mais de um período de tempo. São eles: Juros Simples e Juros Compostos.
Nesse caso, a taxa de juros incide apenas sobre o capital inicial. Exemplificando: se a taxa de juros for de 10% ao ano e o valor presente, que corresponde ao ano 1, for R$ 1000,00. A cada ano, essa taxa incidirá sobre esse valor inicial, do primeiro ano. Portanto, o valor dos juros será sempre o mesmo; nesse caso, igual a:
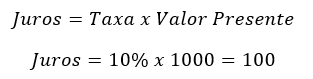
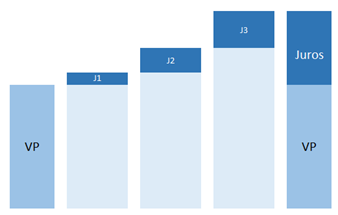
Assim, a cada ano, esse montante fixo é acrescido ao valor inicial – ou valor presente (VP) – e irá compor o montante final, ou valor futuro (VF), conforme a imagem abaixo.
Como o crescimento do montante é constante ao longo do tempo, diz-se que o crescimento ocorre de forma linear.
A principal fórmula dos juros simples é uma mera decorrência do que foi descrito até aqui:
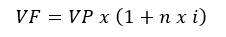
Em que:
VF é o valor futuro;
VP é o valor presente;
n é o número de períodos
i é a taxa de juros.
Na capitalização por juros compostos, a taxa de juros incide sobre o valor inicial acrescido dos juros do período anterior. Como o valor em cima do qual se aplica a taxa de juros aumenta a cada período, os juros também aumentam a cada período.
A imagem abaixo ilustra esse fato, mostrando que os juros correspondentes ao primeiro período, J1, são menores do que o do segundo período, J2 e assim sucessivamente. Nesse caso, diz-se que o crescimento do montante acumulado cresce exponencialmente.
A fórmula para calcular os juros compostos é a seguinte:
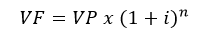
Em que:
VF é o valor futuro;
VP é o valor presente;
n é o número de períodos
i é a taxa de juros.
Os juros simples são calculados sobre o valor inicial da operação, enquanto os juros compostos são calculados sobre o valor inicial mais os juros que já foram cobrados sobre ele – é o chamado “juros sobre juros”.
Os juros compostos são mais comuns em investimentos a longo prazo, pois, com o passar do tempo, os juros vão se acumulando e ficando cada vez maiores. Já nos juros simples, não importa quantos períodos se passam: o valor dos juros acrescido ao valor inicial é sempre o mesmo.
No caso dos empréstimos, os juros compostos podem representar um perigo para o devedor desavisado, pois o efeito acumulativo pode transformar uma pequena dívida em um problema, devido ao efeito do tempo.
Geralmente, os juros compostos são os mais utilizados, tanto para empréstimos quanto para investimentos, no mercado financeiro. Contudo, algumas operações utilizam os juros simples, a exemplo de empréstimos de curto prazo e cobrança de impostos atrasados.
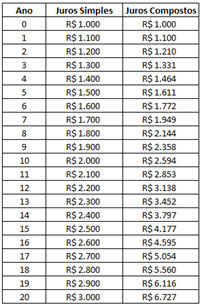
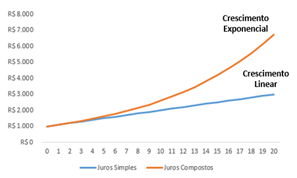
A tabela e o gráfico abaixo ilustram a diferença de crescimento.
Os sistemas de amortização são um assunto de aplicação bastante prática no dia a dia, principalmente quando da aquisição de imóveis via financiamento. Além de buscar no mercado os menores juros, é necessário também compreender qual é o sistema de amortização mais adequado para realizar os pagamentos.
Existem basicamente duas opções:
1) Sistema francês, também conhecido como Tabela Price;
2) Sistema de amortização constante, ou modelo SAC.
Antes de passar ao detalhamento de cada um deles, é importante entender que o valor da parcela a ser paga no processo de quitação do financiamento é composto por dois componentes:
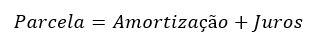
A amortização é a parte da parcela que será utilizada para efetivamente reduzir a dívida. A outra parte da parcela, os juros, são calculados sobre o saldo devedor inicial de cada período e representam a remuneração paga à instituição que concedeu o empréstimo.
Tanto no Sistema francês quanto no SAC, o saldo devedor vai sendo reduzido a cada pagamento de parcela – graças à parcela referente à amortização. Com isso, reduz-se também o valor dos juros incorridos. A diferença entre os dois sistemas está na forma e rapidez da amortização.
Quanto maior for a amortização em um dado período, menor será o saldo devedor e, consequentemente, menor será a parcela dos juros para o período subsequente.
No Sistema francês, a prestação a ser paga durante o período de financiamento é constante, ao passo que a amortização e os juros são variáveis. Como os juros são sempre decrescentes (já que o saldo devedor sempre diminui, devido à amortização paga a cada parcela), a amortização, nesse caso, é crescente.
No SAC, como a amortização é constante e os juros são sempre decrescentes, a parcela também é decrescente. Isso significa que, a cada prestação, um valor idêntico é utilizado para reduzir o valor da dívida.
Assim, por exemplo, em um financiamento de R$ 300 mil em 300 meses, R$ 1 mil serão destinados para a amortização a cada mês. Para encontrar o valor de cada parcela, é necessário, mês a mês, calcular os juros sobre o saldo devedor.
Comparativamente ao Sistema francês, as parcelas iniciais do SAC costumam ser mais altas, e a amortização, mais agressiva. Assim, com o passar do tempo, as prestações do SAC vão diminuindo, enquanto as do PRICE se mantêm constantes.
Um fluxo de caixa representa entradas e saídas de dinheiro ao longo do tempo. Geralmente, é ilustrado, como na imagem abaixo, em que as setas apontadas para baixo representam as saídas de caixa, e as apontadas para cima simbolizam entradas de caixa.
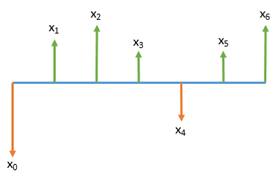
Como o valor do dinheiro muda no tempo, a mera soma dos valores apresentados, denominada soma atemporal, não é suficiente para avaliar o saldo final entre as entradas e saídas. Essa análise só é possível se todos os valores forem deslocados para um mesmo momento no tempo – normalmente, para o momento inicial.
Para fazer esses deslocamentos, divide-se cada um dos valores pelo fator abaixo:
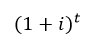
Em que t é o número de períodos de tempo em que a parcela será deslocada e i é a taxa de juros utilizada.
Assim, por exemplo, para deslocar a parcela x1 para o mesmo período de x0, deve-se fazer a seguinte divisão:
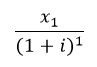
Nesse caso, t = 1, pois apenas um período de tempo separa x1 do período inicial, em que x0 se encontra.
Já no deslocamento de x2 para o período inicial, t = 2, pois essa é a distância temporal entre as parcelas. Assim, a divisão seria:
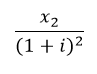
Seguindo a mesma lógica para todas as parcelas componentes desse fluxo de caixa, chega-se ao conceito de Valor Presente Líquido (VPL), que corresponde à soma temporal abaixo:
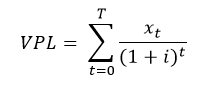
Em que:
T é o período final do fluxo de caixa
i é uma taxa de juros.
A Taxa Interna de Retorno (TIR) é simplesmente a taxa de juros que zera o VPL. Ou seja:
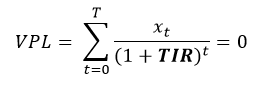
E assim finalizamos mais um artigo, pessoal! Desejo ótimos estudos a todos! Até a próxima!
Lara Dourado
APROVEITE AS OFERTAS DE NOSSAS ASSINATURAS
No Resumo da Semana você encontra diversas informações sobre concursos públicos previstos e editais publicados!…
Salários iniciais podem ultrapassar os R$ 36 mil! Estamos na reta final de 2024 e…
Foi publicado o novo edital do concurso Taubaté Saúde, prefeitura localizada no estado de São…
Quem estuda para concursos públicos sabe que, com a correria do dia a dia, às…
Foi publicado o edital de concurso público do Ituprev (Instituto de Previdência Social dos Servidores…
O governador do estado do Piauí, Rafael Fonteles, informou nas redes sociais que o próximo…