Gabarito PF Estatística: Agente, Escrivão e Papiloscopista

Olá! Tudo bem? 

Como foi a prova da PF? A parte de estatística veio bem pesada, né? Ou você estava bem preparado? 

A seguir, o professor de Estatística do Estratégia, Djefferson Maranhão, e eu apresentamos os nossos comentários das questões 38 a 48. Atente-se aos enunciados, pois a ordem das questões em cada bloco pode ter sido diferente na sua prova.

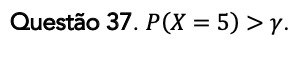
Comentários:

O enunciado informa que a variável é contínua. Para esse tipo de variável, a probabilidade de ela assumir exatamente determinado valor é nula:

P(X = 5) = 0

Resposta: Errado.

Questão 38. O valor esperado de X é igual a 12.

Comentários:

O valor esperado de X é dado por:

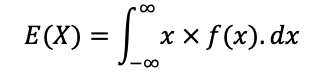
Para isso, precisamos calcular o valor de , considerando-se que a probabilidade associada a todo o Espaço Amostral (U) é igual a 1. Como a variável assume valor no intervalo [0,24) temos:

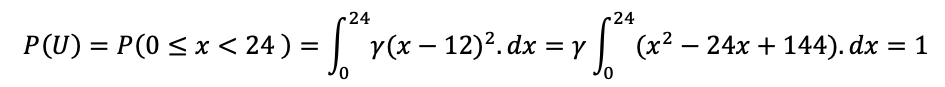
Calculando as integrais em separado (sem aplicar os limites), temos:

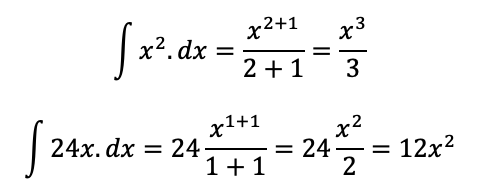
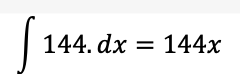
Juntando os termos:

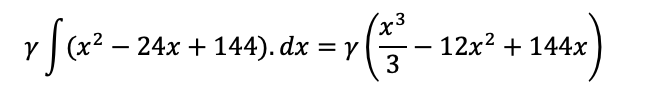
Aplicando os limites da integral, temos:

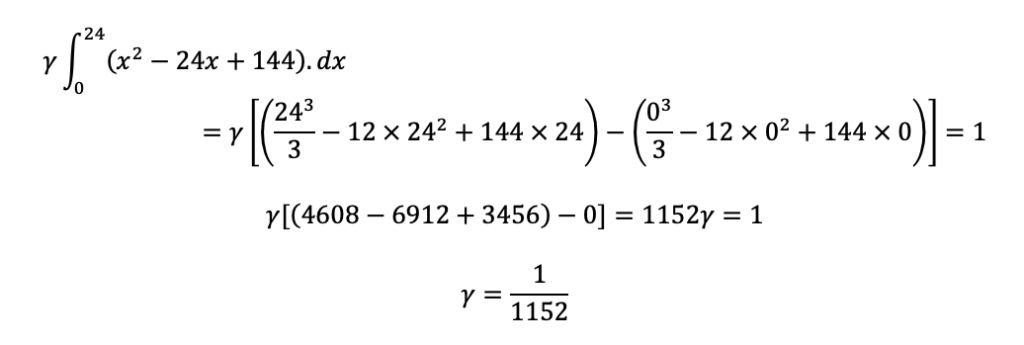
Observação: Se, na expressão acima, você isolar 24×24, as contas ficam menores:

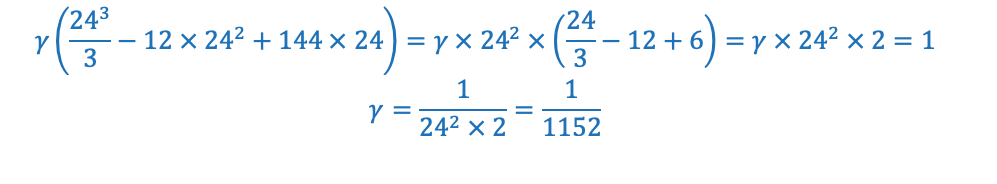
Portanto, conhecendo f(x), o valor esperado é dado por:

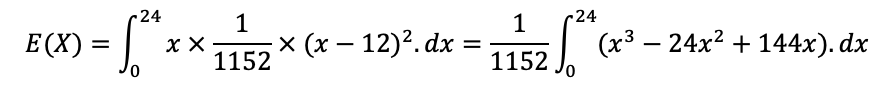
Calculando as integrais em separado (sem aplicar os limites), temos:

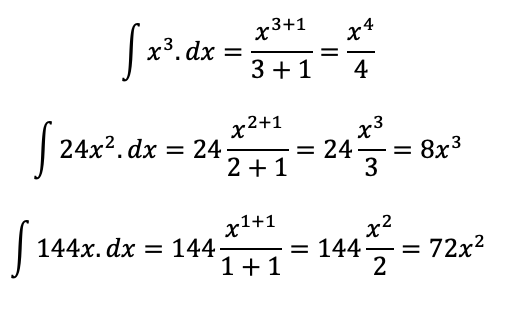
Juntando os termos:

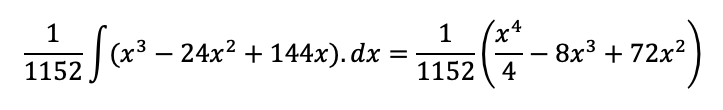
Aplicando os limites da integral, temos:

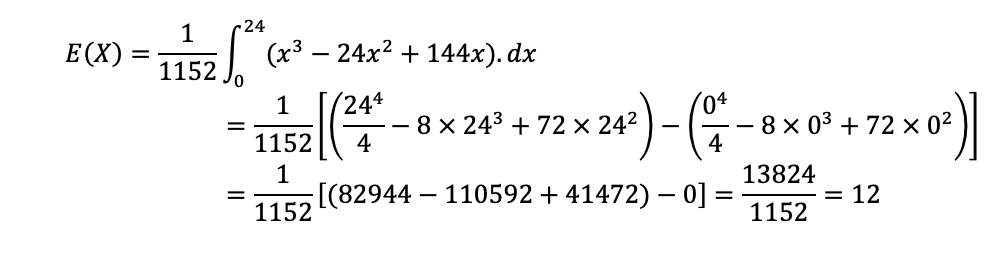
Observação: Similarmente ao que fizemos antes, se você isolar 24x24x24 na expressão acima, as contas simplificam:

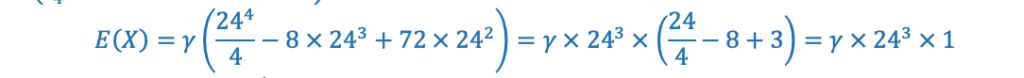
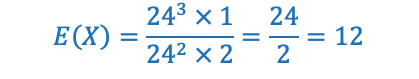
Resposta: Certo.

Comentários:

Na questão anterior, vimos que a constante é:

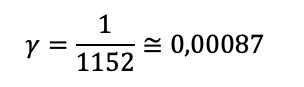
Ou seja, é inferior a 0,01.

Resposta: Certo.

Considere que X e Y sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade

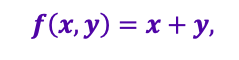
Na qual 0<x<1 e 0<y<1

Com base nessas informações, julgue os itens seguintes.

Questão 40. X e Y são variáveis aleatórias independentes.

Comentários:

Duas variáveis contínuas são independentes quando a função densidade de probabilidade conjunta, f(x,y), é o produto das funções densidade de probabilidade marginal das variáveis:

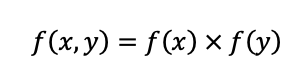
Ou seja, precisamos calcular as funções densidade de probabilidade marginal das variáveis. A função marginal de x é dada por:

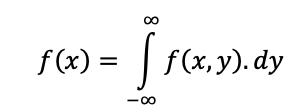
Aqui, estamos integrando em relação a y, ou seja, x é considerada constante. Calculando a integral, sem considerar os limites, temos:

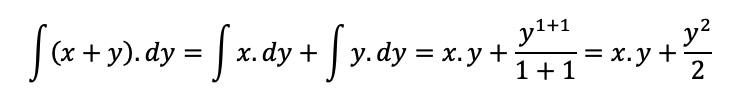
Aplicando os limites,temos:

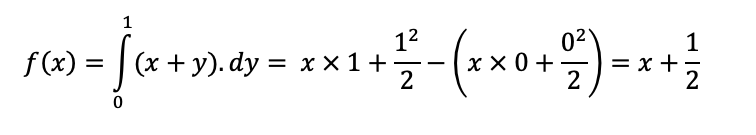
A função marginal de y é dada por:

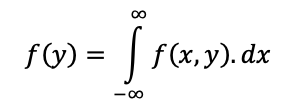
Ou seja, temos uma integral em relação a x, em que consideramos y constante. Calculando a integral, sem considerar os limites, temos:

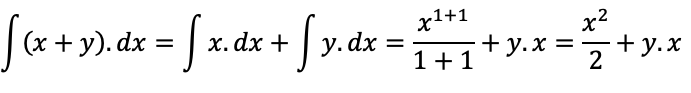
Aplicando os limites, temos:

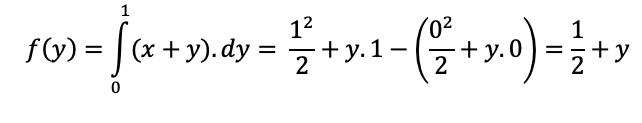
O produto das funções marginais é:

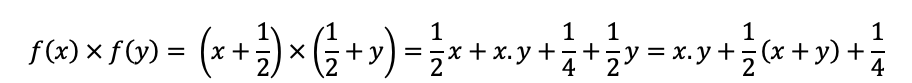
Podemos observar que essa função é diferente da função densidade conjunta fornecida. Por esse motivo, as variáveis não são independentes.

Resposta: Errado.

Questão 41. Y é uma variável uniforme no intervalo (0,1)

Comentários:

Na questão anterior, calculamos que a função densidade marginal de y é:

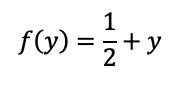
Ou seja, quando y=0 a função é f(y)=1/2 e quando y=1 a função é f(y)=1+1/2=3/2. Logo, o valor da função varia, não sendo, portanto, uniforme.

Resposta: Errado.

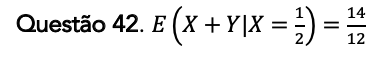
Comentários:

A questão está pedindo pela esperança de Y condicionada a X=1/2. Antes de entrar nos cálculos, podemos aplicar a propriedade aditiva da integral para facilitar as nossas contas:

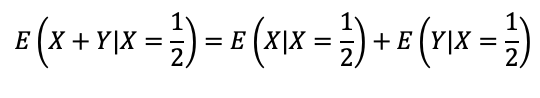
Sabendo que  x=1/2, a esperança de X é igual a 1/2:

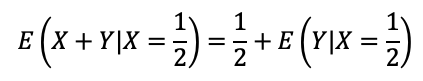
A esperança de Y, condicionada a X = x, é dada por:

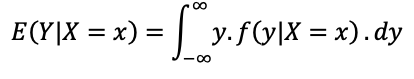
Em que f(y|x) é a função densidade de Y condicionada a X, que é a razão entre a função densidade conjunta e a função marginal de x:

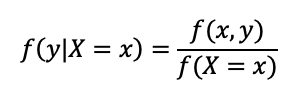
Já calculamos f(x)=x+1/2, então, o valor de f(X=1/2) é:

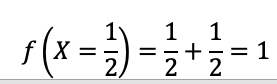
Portanto, a função de Y condicionada a X=1/2 é:

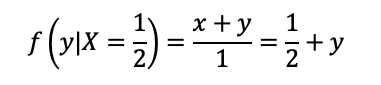
Agora, podemos calcular a esperança de Y condicionada a X=1/2:

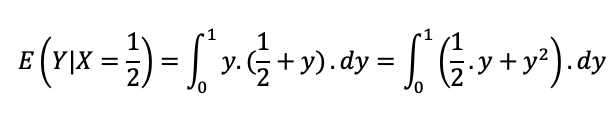
Calculando as integrais em separado, sem considerar os limites, temos:

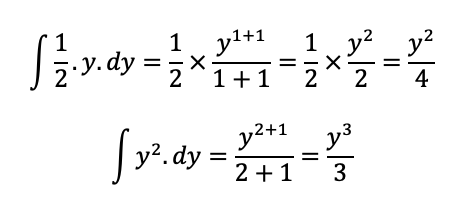
Juntando as expressões, temos:

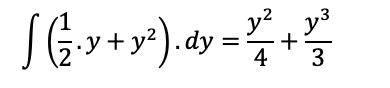
Aplicando os limites, temos:

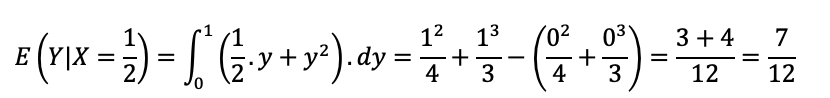
Por fim, somamos E(X|X=1/2) para obter E(X+Y|X=1/2):

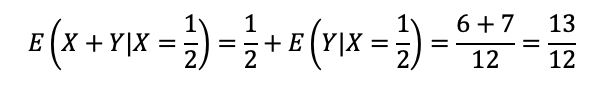
O resultado é diferente de 14/12.

Resposta: Errado.

Comentários:

Uma estatística é considerada suficiente quando se ela captura, a partir da amostra obtida, toda a informação possível sobre o parâmetro populacional desconhecido, de modo que qualquer outra informação não contribuirá com a estimação do parâmetro populacional. 

Considerando que o enunciado forneceu a função de distribuição acumulada, o parâmetro pode ser estimado a partir da mediana da distribuição, a função de distribuição acumulada é igual a 0,5:

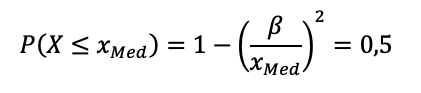
A partir dessa equação, é possível calcular o valor do parâmetro . Ou seja, precisamos da mediana da distribuição, e não da média. Portanto, a média não é uma estatística suficiente para estimar esse parâmetro.

Resposta: Errado.

Questão 44. Pelo método dos mínimos quadrados ordinários, a estimativa da média populacional é igual ou superior a 3,5. 

Comentários:

A estimativa da média populacional pelo método dos mínimos quadrados é a média amostral, dada por:

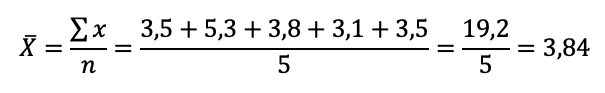
Como 3,84 é superior a 3,5, o item está certo.

Resposta: Certo.

Comentários:

Agora, vamos voltar ao cálculo da mediana, utilizando a estimativa da mediana observada. Para isso, vamos ordenar os valores observados:

3,1

3,5

3,5

3,8

5,3

Podemos observar que a mediana é igual a 3,5, logo:

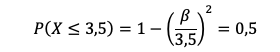
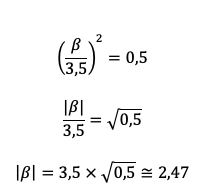
Portanto, o parâmetro é inferior a 3,5

Resposta: Errado.

Um estudo objetivou avaliar a evolução do número mensal Y de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples de forma

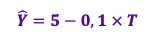
Os erros padrão das estimativas dos coeficientes desse modelo, as razões t e seus respectivos p-valores encontram-se na tabela a seguir:

	erro padrão	razão	p-valor
intercepto	0,584	8,547	0,00
coeficiente angular	0,064	1,563	0,15

Os desvios padrão amostrais das variáveis Ye T foram, respectivamente, 1 e 3,6.

Com base nessas informações, julgue os itens a seguir.

Questão 46. Se a média amostral da variável T for igual a 6,5, então a média amostral da variável Y será igual a 4,35 mil ocorrências.

Comentários:

Resposta: Certo.

Comentários:

De fato, como o p-valor da estimativa do coeficiente angular é maior que o nível de significância (0,15 > 0,05), não temos evidências estatísticas suficientes para rejeitar a hipótese nula.

Gabarito: Certo.

Questão 48. A correlação linear entre as variáveis Y e T foi igual a -0,1.

Comentários:

A estimativa de beta, pelo método dos mínimos quadrados, é dada pela expressão:

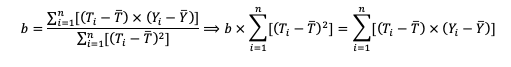
Vamos relacionar essa expressão com a do coeficiente de correlação:

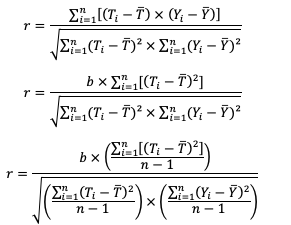
Assim, concluímos que o coeficiente de correlação pode ser expresso por meio da seguinte relação:

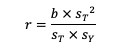
Logo, temos o seguinte coeficiente de correlação:

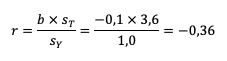
Gabarito: Errado.