Estatística Descritiva para a SEFAZ-PA
Revise, nessa reta final, os principais tópicos cobrados no Edital, relacionados à Estatística Descritiva, para o concurso da SEFAZ-PA.
Olá, pessoal! O edital da SEFA PA (Secretaria do Estado da Fazenda do Pará) é mais uma grande oportunidade para a área fiscal! Nesse momento de reta final, cada detalhe pode fazer a diferença rumo à sonhada aprovação; portanto, é hora de entregar tudo!
O tema do artigo de hoje, Estatística Descritiva, está presente para os dois cargos do concurso (Auditor Fiscal de Receitas Estaduais e Fiscal de Receitas Estaduais).
Inicialmente, iremos contextualizar o assunto dentro do universo maior da Estatística e, em seguida, aprofundaremos nos tópicos expressamente citados no edital.
Ramos da Estatística – Estatística Descritiva para a SEFAZ-PA
Estatística é a ciência de coletar, analisar e interpretar dados em grandes quantidades, normalmente com o propósito de fazer predições a respeito de uma população com base em uma amostra representativa.
Existem dois ramos da Estatística: a Estatística Descritiva e a Inferencial. Tipicamente, ao fazer a análise de um determinado conjunto de dados, utilizam-se ambas para tirar conclusões.
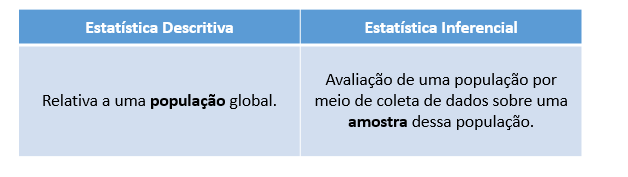
Estatística Descritiva
Esse ramo provê informações imediatas sobre um grupo de dados. Por exemplo, se o Estratégia quiser analisar o desempenho de 200 alunos em determinada prova de concurso, é possível calcular a média das suas notas finais. Essa média traria uma informação bastante valiosa a respeito desse grupo específico de 200 alunos.
Um conjunto como esse, que abrange todos os dados de interesse de uma análise, é denominado população. A Estatística Descritiva é aplicada a populações, e as propriedades que são calculadas, como a média ou o desvio padrão, são os parâmetros, que representam toda a população.
No entanto, nem sempre é possível ter acesso a dados de toda a população de interesse, seja por limitação de tempo para fazer a análise, seja por dificuldades de coleta. Nesses casos, entra em cena a Estatística Inferencial.
Estatística Inferencial
A Estatística Inferencial utiliza uma amostra de dados retirados de uma população para descrever e fazer inferências sobre a população.
As propriedades da amostra, tais como a média ou o desvio padrão, não são parâmetros, e sim estatísticas.
Esse ramo da Estatística lança mão de técnicas que permitem que as amostras sejam utilizadas para fazer generalizações sobre a população da qual a amostra foi retirada.
Por exemplo, o Estratégia pode medir o desempenho de um pequeno grupo, utilizando-o para representar a população inteira de seus alunos. Para que esse procedimento dê certo, é preciso que a amostra represente de forma acurada a população.
O processo de chegar a um grupo representativo do todo é chamado de amostragem, que, por sua vez, naturalmente incorre em erros, já que não é esperado que a amostra represente perfeitamente a população.
Uma das principais limitações da Estatística Inferencial é justamente não ter 100% de confiança de que as estatísticas calculadas estão corretas, pois sempre haverá um grau de incerteza ao usar valores medidos em uma amostra para estimar/inferir os valores que seriam medidos em uma população.
Aprofundando a Estatística Descritiva para a SEFAZ-PA
Na era do Big Data, Ciência de Dados e Inteligência Artificial, a análise de grandes quantidades de dados tornou-se essencial em muitos campos da ciência e da tecnologia.
A Estatística Descritiva aborda um aspecto extremamente necessário ao trabalhar com dados, que é a habilidade para descrever, resumir e representar dados visualmente, de modo a facilitar o entendimento. Ressalta-se que isso não envolve qualquer generalização ou inferência além do que está disponível.
Em um cenário, por exemplo, em que são coletados dados de milhões de pessoas, não é humanamente prático se debruçar na leitura de tantas informações. Ainda que alguém de boa vontade se dispusesse a ler todos esses dados, dificilmente seria capaz de extrair informações úteis a partir deles.
Por outro lado, ao fazer um simples resumo, levantando informações como salário médio ou idade média, já é possível tirar conclusões e, se necessário, aprofundar as análises a partir daí.
Assim, a Estatística Descritiva representa um “pacote básico” de informações que são úteis para a análise de qualquer conjunto de dados, dos mais simples aos mais sofisticados. Suas medidas fornecem uma ideia geral de tendências nos dados e possibilitam a emersão de padrões que não seriam óbvios se apenas os dados brutos fossem apresentados.
Tipicamente, existem dois tipos gerais de medidas que são utilizadas para descrever os dados:
- Medidas de Tendência Central ou Posição: representam um valor único, que pretende resumir um conjunto de dados, identificando a sua posição central.
- Medidas de Dispersão ou Variabilidade: resumem um grupo de dados através da descrição do quão espalhados seus valores estão em torno do valor central (ou das Medidas de Tendência Central).
A seguir, serão descritas algumas medidas pertencentes a cada um desses grupos.
Medidas de posição
Média – Estatística Descritiva para a SEFAZ-PA
A Média é a medida de posição central mais conhecida. É definida como a razão entre a soma de todos os valores observados no conjunto de dados e número total de observações.
Uma propriedade bastante importante da média é que ela inclui todos os valores do conjunto de dados em seu cálculo. Como consequência, ela é particularmente suscetível à influência de outliers, que são aqueles pontos muito fora da curva.
Por exemplo, considerando os salários dos empregados de uma empresa, listados abaixo:

A média dos salários é igual a R$3.070,00. Porém, ao analisar os dados brutos, nota-se que essa média pode não ser o melhor valor para refletir o salário típico de um trabalhador desse grupo, pois a maioria tem salários na faixa entre R$1.200,00 e R$1.800,00.
Mediana – Estatística Descritiva para a SEFAZ-PA
A Mediana é o ponto que divide todos os dados em duas metades iguais. Dessa forma, metade dos valores será menor do que a Mediana, e a outra metade será maior. Para calcular a Mediana, é necessário primeiramente ordenar os dados.
- Se o número de observações for ímpar, a Mediana é dada pelo ponto que estiver no centro dos dados ordenados;

- Se o número de observações for par, a Mediana é dada pela média das duas observações centrais dos dados ordenados.
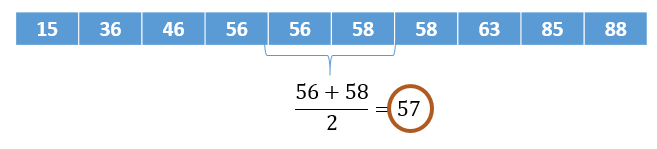
Um ponto de atenção é que a mediana é menos afetada por outliers e dados distorcidos, já que esses ficam situados nos extremos e, assim, não entram no cálculo da mediana.
Moda – Estatística Descritiva para a SEFAZ-PA
Moda é o número mais frequente no conjunto de dados, ou, em outras palavras, é aquele que mais aparece. Um conjunto de dados pode possuir uma ou mais modas:
- Se existe apenas um número que apareça o máximo de vezes, o conjunto de dados possui apenas uma moda, sendo denominado unimodal;
- Se existem dois números que são igualmente mais frequentes, os dados possuem duas modas, e o conjunto é denominado bimodal;
- Se existem mais de dois números que possuem a frequência máxima, os dados possuem mais do que duas modas, e o conjunto é chamado multimodal.
É possível também que uma sequência não possua Moda, caso nenhum valor se repita mais frequentemente do que os demais.
Medidas de variabilidade
Desvio Absoluto Médio – Estatística Descritiva para a SEFAZ-PA
O Desvio Absoluto Médio corresponde a uma média das distâncias de cada observação com relação à Média. Assim, para calculá-lo, primeiramente determina-se o quanto cada ponto está afastado da Média; depois, basta somar esses valores e dividir pelo total de pontos do conjunto de dados.
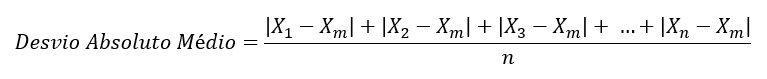
Desvio Padrão e Variância – Estatística Descritiva para a SEFAZ-PA
O Desvio Padrão mede o quão os pontos de uma sequência de dados estão distantes, ou espalhados, da Média. Dessa forma, um Desvio Padrão alto indica que os pontos estão muito espalhados, enquanto um Desvio Padrão pequeno indica que os pontos estão mais próximos da Média do conjunto.
Para obter o Desvio Padrão deve-se, inicialmente, calcular as distâncias de cada um dos pontos à Média – até aqui, exatamente o que é feito para o cálculo do Desvio Absoluto. Em seguida, é necessário também elevar ao quadrado cada uma dessas distâncias.
Esse procedimento confere um peso especial à existência de valores mais distantes da Média, já que, ao multiplicar a distância por ela mesma, as distâncias maiores terão maior impacto no cálculo final.
Ao somar todas essas distâncias elevadas ao quadrado e dividir pelo número de observações, chega-se a uma medida denominada Variância. Essa medida é menos usada na Estatística Descritiva, pois, ao utilizar valores elevados ao quadrado, sua escala de grandeza difere daquela dos valores do conjunto de dados.
Portanto, para que o Desvio Padrão seja comparável aos demais valores da sequência que está sendo analisada, o último passo do seu cálculo é obter a raiz quadrada da Variância.
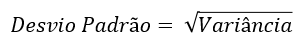
Quartis – Estatística Descritiva para a SEFAZ-PA
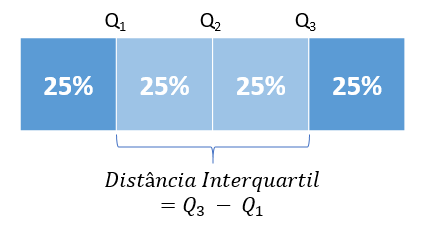
Quartis são pontos que dividem o conjunto de dados em quatro partes iguais. Assim, sendo Q1, Q2 e Q3, respectivamente, o primeiro, o segundo e o terceiro quartil do conjunto:
- 25% dos pontos do conjunto estão abaixo de Q1 e 75% estão acima dele;
- 50% dos pontos do conjunto estão abaixo de Q2 e 50% estão acima dele – sim, Q2 é a Mediana!
- 75% dos pontos do conjunto estão abaixo de Q3 e 25% estão acima dele.
A distância entre Q1 e Q3 chama-se Distância Interquartil.
Gráficos – Estatística Descritiva para a SEFAZ-PA
Como já discutido, a Estatística Descritiva trata de descrever os dados para melhor compreendê-los. Um típico fluxo do processo de análise de um conjunto de dados consiste, inicialmente, na avaliação das medidas de tendência central e de variabilidade. Após essa primeira ideia geral, é importante visualizar os dados, utilizando gráficos.
Selecionar o gráfico mais apropriado não é uma tarefa tão óbvia ou pragmática. Existem literalmente dezenas de opções, e a melhor escolha depende do tipo de dado que está sendo analisado e do que se deseja descobrir a partir dele. Muitas vezes, a experiência da pessoa que conhece bem o contexto do qual os dados foram coletados é imprescindível.
No entanto, o conhecimento do tipo de variável em estudo facilita essa escolha. Existem dois principais tipos de variáveis:
- Variáveis categóricas: também são chamadas de atributos, qualidades, dimensões ou variáveis qualitativas. Normalmente decorrem de classificações associadas aos objetos analisados.
- Variáveis quantitativas: podem ser chamadas de medidas e apresentam valores numéricos.
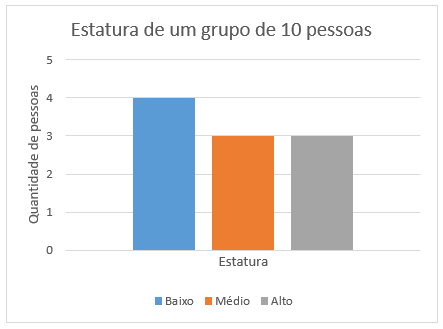
Uma única variável categórica é geralmente representada por um gráfico de barras.
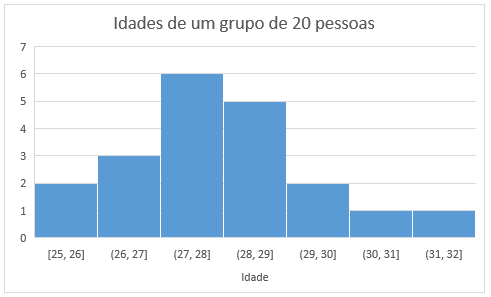
Uma única variável numérica pode ser visualizada com um histograma.
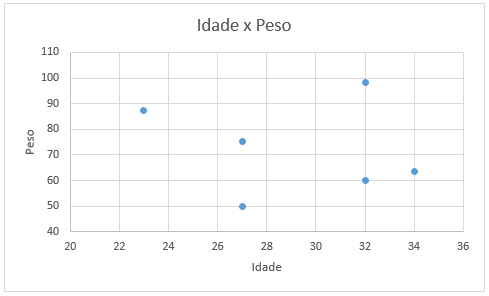
Para duas variáveis numéricas, é interessante utilizar um gráfico de dispersão.
E assim finalizamos mais um artigo! Bons estudos e até a próxima!
Lara Dourado