Confira nesse artigo dicas sobre um problema que pode cair na sua prova de matemática ou de raciocínio lógico: como calcular a área dos principais polígonos?
Olá, pessoal, tudo bem?
Hoje vamos falar sobre uma dúvida comum entre os alunos. Afinal, como se calcula a área de um polígono?
Para um melhor entendimento do assunto, trataremos dos seguintes tópicos:
Em primeiro lugar, vamos estabelecer algumas definições básicas.
Conforme o Dicionário Oxford, polígono é qualquer figura plana formada pelo mesmo número de ângulos e de lados retos. Por exemplo, a seguir, temos um retângulo, um tipo de quadrilátero irregular:
Na figura acima, observamos que o retângulo é uma figura plana, isto é, circunscrita em um ambiente bidimensional. Ademais, essa figura possui quatro lados retos e quatro ângulos. Desse modo, concluímos que o retângulo é um polígono.
Além disso, os polígonos podem ser regulares ou irregulares. Quanto a esse assunto, não há mistério, uma vez que os polígonos regulares são definidos pelo fato de possuírem lados e ângulos iguais. Por outro lado, os polígonos irregulares podem apresentar lados e ângulos diferentes.
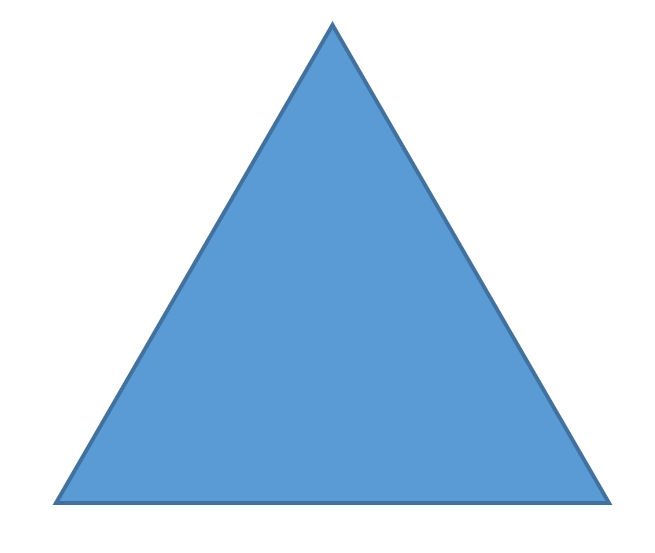
Na figura acima, temos um polígono com lados e ângulos iguais. Desse modo, trata-se de um polígono regular.
Em contrapartida, na figura do retângulo, notamos um polígono que, mesmo possuindo ângulos iguais, possui lados diferentes. Assim sendo, trata-se de um polígono irregular, já que não cumpre todas as exigências da definição dos polígonos regulares.
Segundo Machado (2012), o conceito de área está, intuitivamente, ligado à ideia de ocupação de uma região do plano delimitada por um contorno.
Voltando a figura do quadrilátero, percebemos, então, que a área dessa figura é a região que é delimitada pelo contorno dos lados desse polígono.
Após as definições básicas, partamos para o cálculo, de fato, das áreas dos principais polígonos. Vale destacar que nos deteremos, principalmente, na análise de polígonos regulares nesse artigo.
Primeiramente, confira a figura a seguir:
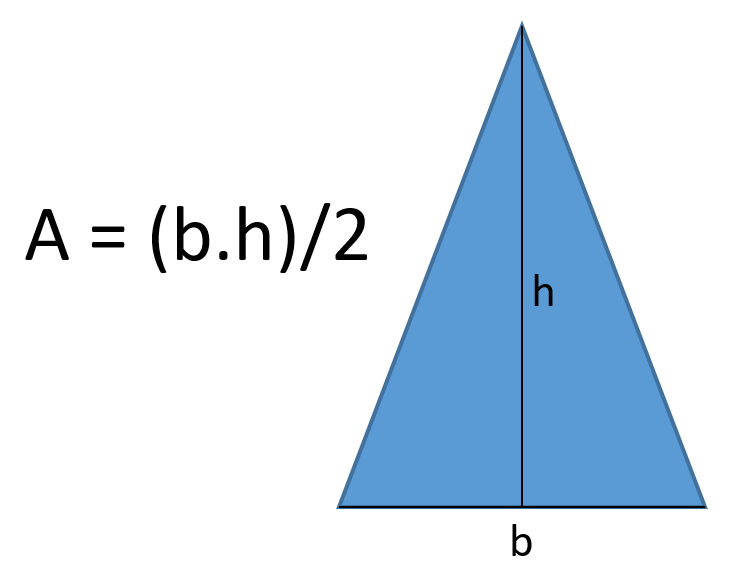
Nessa figura, notamos que o triângulo possui uma base e uma altura. Para o cálculo da área, devemos multiplicar a base pela altura, dividindo o valor obtido por dois. Dessa forma, obtemos o valor da área do triângulo.
Além disso, destaca-se que saber encontrar a área do triângulo é fundamental, já que as áreas de diversos outros polígonos podem ser encontradas decompondo esses polígonos em triângulos.
Em seguida, temos o quadrilátero regular:
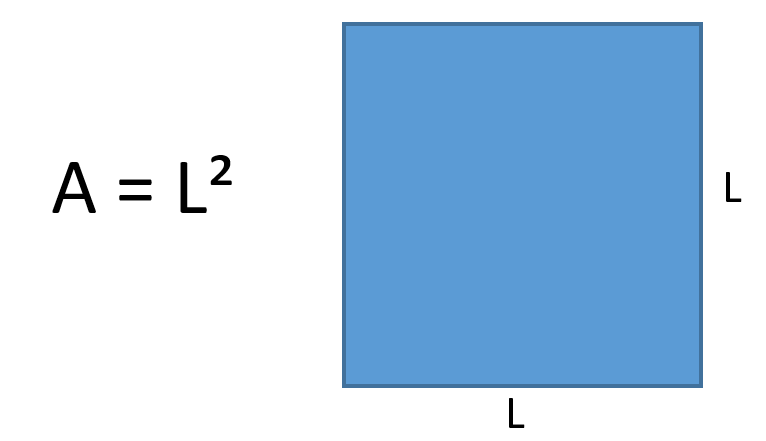
Do polígono acima, notamos que o quadrilátero regular, vulgo quadrado, possui lados iguais. Para o cálculo de sua área, devemos multiplicar um lado pelo outro, obtendo, assim, o valor da área do quadrilátero.
Por uma diferente ótica, podemos dizer, também, que a área pode ser calculada pelo produto entre a base e a altura do quadrilátero.
Ademais, vale destacar que todo quadrado é um quadrilátero. No entanto, nem todo quadrilátero é um quadrado. Essa diferenciação é um clássico “peguinha” de prova e o concurseiro deve, assim, estar atento a isso.
Por fim, embora não seja um polígono regular, as áreas dos retângulos e dos paralelogramos podem, também, ser calculadas pelo produto da base pela altura.
Dentre os principais polígonos, temos o pentágono.
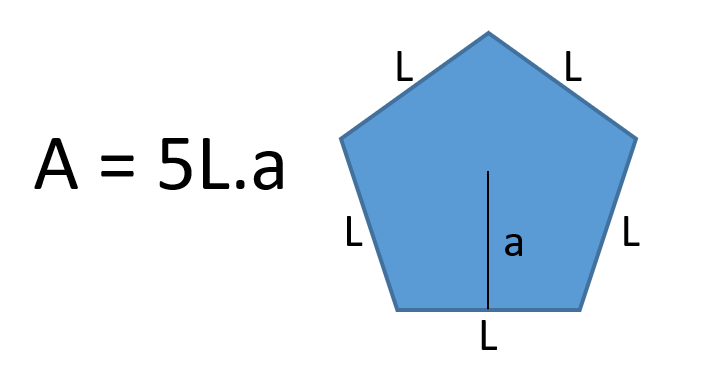
Em outras palavras, a área do pentágono é calculada multiplicando o perímetro do polígono pelo seu apótema. Vale pontuar que o apótema é um segmento de reta que vai do centro do polígono regular até o centro de um dos lados do pentágono.
Quanto ao hexágono, temos que:
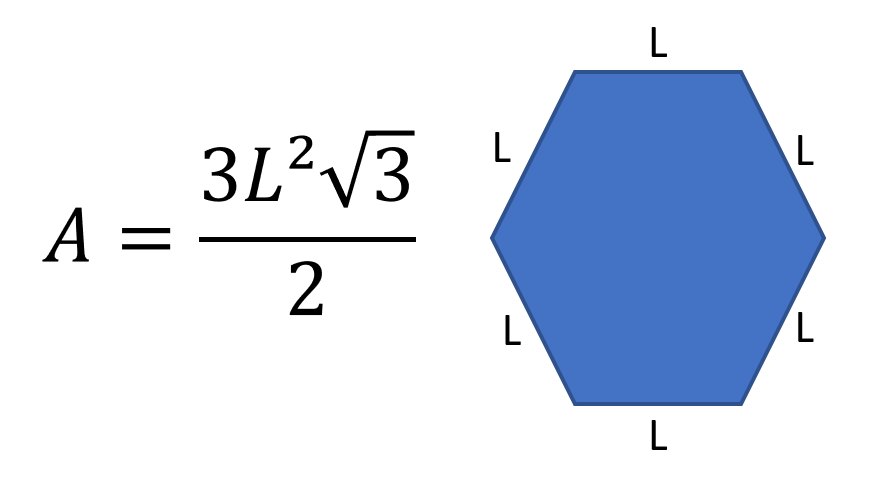
Nessa figura, notamos que basta que saibamos do tamanho do lado do hexágono e da fórmula de sua área.
Ademais, podemos também calcular a área desse polígono dividindo-o em seis triângulos equiláteros. Dessa forma, não seria necessário decorar mais uma fórmula.
Em primeiro lugar, os polígonos que serão apresentados nesse tópico não são regulares. Todavia, em função da importância deles, serão, também, apresentados.
Para esse caso, segue que:
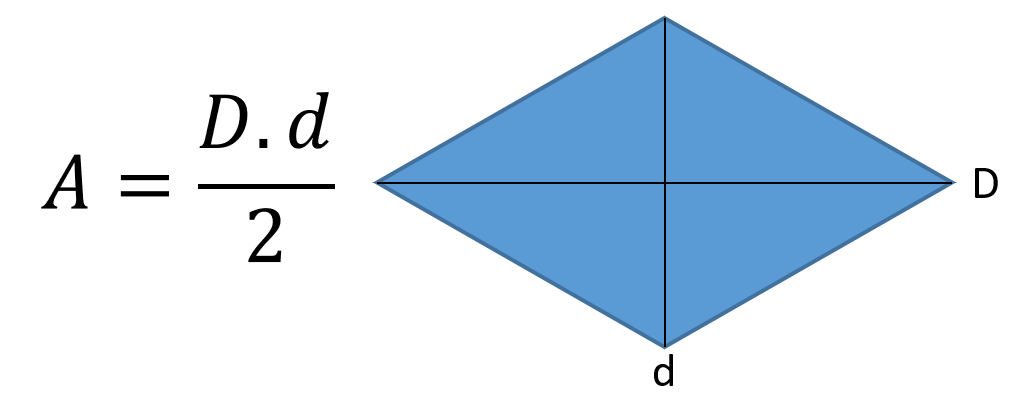
Da figura acima, observamos que podemos traçar duas diagonais no losango. Para o cálculo da área desse polígono, basta que multipliquemos a suas duas diagonais e dividamos o resultado por dois.
Em relação ao trapézio, temos que:
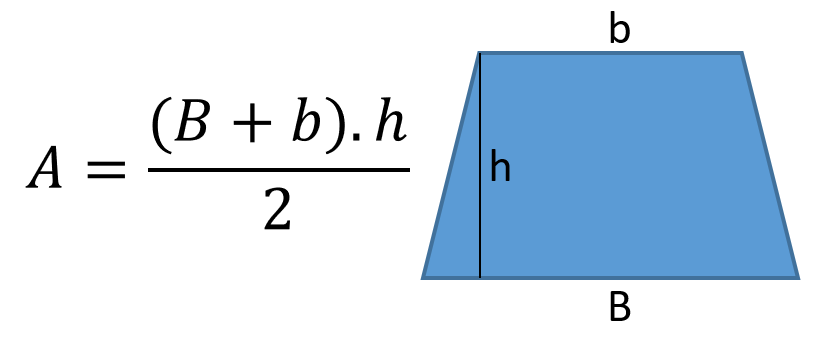
Nessa figura, percebemos que a área do trapézio é definida em função da soma de sua base maior com sua base menor. Esse resultado multiplicado pela altura do trapézio e dividido por dois nos fornece a área do trapézio.
Primeiramente, no artigo de hoje, buscamos tirar uma dúvida que muitas pessoas têm: como calcular a área dos principais polígonos?
Sem dúvida, não se trata de uma questão de muita complexidade. No entanto, o cálculo das áreas dos polígonos requer prática do aluno, principalmente para os polígonos que costumam ser menos cobrados em prova.
Ademais, para os alunos que têm dificuldades com fórmulas, uma dica é tentar dividir o polígono em triângulos. Desse modo, é possível, muitas vezes, resolver a questão somente sabendo a fórmula da área do triângulo e um pouco de lógica.
Enfim, caso esse assunto esteja listado no seu edital, não deixe ele para segundo plano, buscando fazer muitos exercícios para auxiliar na memorização das principais fórmulas.
No mais, desejo a todos paz, saúde e foco nos estudos!
Um grande abraço!!
MACHADO, P. F. Fundamentos de Geometria Plana. Belo Horizonte: CAEDE-UFMG, 2012.
Assinatura Anual Ilimitada*
Prepare-se com o melhor material e com quem, certamente, mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha, desse modo, acesso ilimitado* a todos os nossos cursos.
ASSINE AGORA – Assinatura Ilimitada
Fique por dentro de todos os concursos:
Se você está ligad@ aqui no Estratégia Carreiras Jurídicas, sabe a aprovação está no horizonte proximo!…
O concurso do Ministério Público do Paraná (MP PR) ocorreu no último domingo de setembro…
Os resultados preliminares das provas objetivas do concurso TRF 5 (Tribunal Regional Federal da 5ª Região) já…
Resultados preliminares das provas objetivas disponíveis O concurso do Tribunal Regional Federal da 5ª Região…
Oportunidades em todos os níveis de escolaridade! Foi divulgado o resultado preliminar da prova discursiva…
* Thiago de Paula Leite é procurador do Estado de São Paulo e professor de…