Aprenda a calcular a mediana de um conjunto de dados

Confira nesse artigo como calcular a mediana de um conjunto de dados. Além disso, entenda as diferenças entre moda, mediana e média.

Olá, pessoal, tudo bem?

Nesse artigo, aprenderemos o que é a mediana e, também, como calculá-la. Ademais, para um melhor entendimento do assunto, trataremos dos seguintes assuntos:

1. O que é mediana?
2. Como calcular a mediana?
3. Qual é a diferença entre média, mediana e moda?
4. Considerações finais

1. O que é mediana?

Conforme exposto pelo professor Guilherme Neves do Estratégia Concursos, a mediana pode ser definida como um número disposto de forma centralizada em uma série de números, organizados segundo uma ordem.

2. Como calcular a mediana?

Mediana para dados não agrupados

Em princípio, vejamos um exemplo de um conjunto de dados não agrupados:

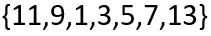
De acordo com a definição de mediana, precisamos ordenar os valores do grupo:

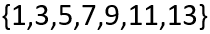
Em seguida, encontremos o elemento central do conjunto. Em outras palavras, aquele membro do conjunto cuja posição marca um ponto em que há um número iguais de elementos à esquerda e à direita desse valor. Por exemplo, para esse conjunto, temos:

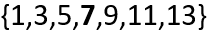
Assim, a mediana do conjunto é o número 7, uma vez que possui o mesmo número de elementos à sua esquerda e à sua direita.

Contudo, nem tudo são flores. No caso acima, a quantidade de elementos era ímpar, o que, certamente, facilita a missão de encontrar o elemento central. Mas, agora, vejamos o seguinte conjunto numérico:

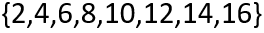
Nesse caso, de fato, você não consegue encontrar apenas um elemento central que divida igualmente o conjunto em dois. Desse modo, para a quantidade par de elementos, devemos encontrar os dois elementos centrais do conjunto:

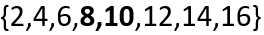
Então, percebemos que os dois números centrais separam dois conjuntos de três elementos. A fim de calcularmos a mediana para esse tipo de caso, devemos fazer a média aritmética dos dois elementos centrais:

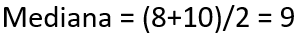
Portanto, para os casos de dados não agrupados, devemos estar muito atentos à ordenação dos elementos e, também, à quantidade de elementos do conjunto (par ou ímpar).

Mediana para dados agrupados sem intervalos de classe

Para esse caso, a mediana pode ser encontrada similarmente ao tópico anterior. Contudo, precisamos ter certos cuidados. Por exemplo, vejamos o seguinte conjunto de dados:

Notas depositadas em um caixa eletrônico no dia x	Frequência	Frequência acumulada
Dois reais	2	2
Cinco reais	1	3

Só para ilustrar, poderíamos representar o conjunto de elementos do exemplo acima da seguinte forma:

Ou seja, duas ocorrências do caso dois reais e uma ocorrência do caso cinco reais. Desse modo, a mediana é dois reais nessa situação.

Em seguida, partamos para uma situação mais complexa:

Notas depositadas em um caixa eletrônico no dia x	Frequência	Frequência acumulada
dois reais	35	35
cinco reais	20	55
dez reais	18	73
vinte reais	15	88
cinquenta reais	8	96
cem reais	4	100

Sem dúvida, poderíamos representar a situação como um conjunto numérico que nem fizemos no exemplo anterior. Todavia, em função da alta quantidade de elementos, isso ocasionaria um dispêndio de tempo considerável (coisa que o concurseiro não tem é tempo, não é mesmo?).

Assim, vejamos uma forma diferente de resolver esse tipo de problema. Primeiramente, somemos a frequência dos eventos (n) e vejamos a quantidade total de elementos:

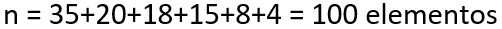
Ademais, sabendo o número de elementos de um conjunto, conseguimos descobrir os seus elementos centrais do seguinte modo:

Nesse exemplo, temos, decerto, um conjunto com um número par de elementos. Dessa forma, segue que:

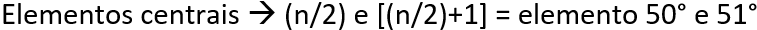
Em seguida, observando a frequência acumulada averiguamos que os elementos 50° e 51° se encontram na classe “cinco reais”. Portanto, conseguimos calcular a mediana do exercício:

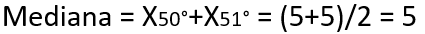
Cálculo da mediana para dados agrupados em classe

Primeiramente, para fins didáticos, vejamos a tabela a seguir:

Quantias depositadas em um caixa eletrônico no dia x	Frequência	Frequência acumulada
zero a dois reais	4	4
dois a quatro reais	2	6
quatro a seis reais	2	8
seis a oito reais	1	9
oito a dez reais	1	10

Em contraste com os tipos anteriores de problemas, esse caso não requer o conhecimento da natureza par ou ímpar dos conjuntos numéricos. Assim sendo, basta que saibamos a frequência acumulada de eventos (n=10) e façamos a seguinte conta para determinar em qual classe a mediana se encontra:

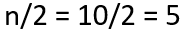
Desse modo, notamos que a mediana não está nas classes de “zero a dois reais” e, sim, na classe de “dois a quatro reais”. Logo, para o cálculo da mediana, precisamos aplicar a seguinte fórmula:

Para que o problema dado, temos os seguintes inputs:

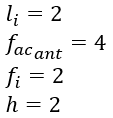
Por fim, aplicando os inputs na fórmula, encontramos a mediana do problema:

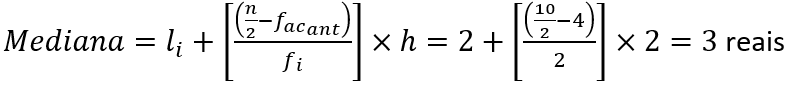
3. Qual é a diferença entre média, mediana e moda?

Média

Primeiramente, comecemos com a média, medida de tendência que possui diversos tipos, tais como as médias aritméticas, harmônicas e ponderadas.

Todavia, em geral, o tipo mais cobrado é a média aritmética, em que todos os números de um conjunto de elementos numéricos são somados e divididos pela quantidade total de elementos.

Moda

Ademais, no que tange à moda, trata-se de outro indicador de tendência central, introduzido por Karl Pearson. Em suma, é uma medida que define o valor ou os valores que se apresentam com maior frequência em um conjunto sob estudo.

Média, mediana e moda

Assim sendo, podemos perceber que a média, a mediana e a moda são medidas diferentes, utilizadas para diferentes fins. Só para exemplificar, tomemos como exemplo o seguinte conjunto numérico:

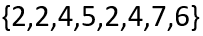
Em primeiro lugar, para uma melhor análise, organizemos o conjunto em ordem crescente:

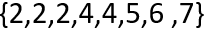
Em seguida, para esse exemplo, encontramos que a média do conjunto é 4 (somatório de todos os valores dividido pelo número de elementos), a mediana é 4 (conforme demonstração feita no tópico anterior) e a moda do conjunto é 2 (por ser o elemento que mais se repete).

Vale destacar que, de fato, uma das principais diferenças entre a mediana e a média reside no fato de que a mediana é uma medida que reflete mais fielmente o centro de um conjunto, não sendo afetada pelos valores extremos.

Por outro lado, a média leva em consideração todos os elementos do conjunto e, assim, é mais afetada pelos chamados “outliers” (aqueles valores que se destacam dos demais). Aliás, se não estiver claro, faça um pequeno experimento: troque o último elemento do conjunto por 950 e veja como a média e a mediana se comportarão.

Por fim, caso ainda reste dúvidas sobre o assunto, confira esse artigo informativo.

4. Considerações finais

Primeiramente, nesse artigo, buscamos trazer algumas dicas de como calcular a mediana de forma simples e rápida.

Ademais, por mais que seja um assunto que não necessite de cálculos complexos, exige uma boa capacidade analítica para saber qual metodologia empregar para encontrar a mediana de um conjunto de dados.

Além disso, lembremos dos cuidados de ordenarmos os dados antes de resolvermos os problemas (nos casos de dados não agrupados e de dados agrupados sem intervalos de classe). Igualmente importante é observarmos se a quantidade de elementos é par ou ímpar, pois isso pode influenciar a forma de “atacar” a questão.

Por fim, desejo a todos fé, dedicação e bons estudos.

Um grande abraço!!

Assinatura Anual Ilimitada*

Prepare-se com o melhor material e com quem, certamente, mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha, desse modo, acesso ilimitado* a todos os nossos cursos.

ASSINE AGORA – Assinatura Ilimitada

Antes de mais nada, fique por dentro de todos os concursos:

Concursos abertos

Concursos 2020