Algoritmo de Ordenação por Seleção – Concurso BB (TI)

Olá pessoal! Tudo bem? Para você que está se preparando para o concurso do Banco do Brasil, cargo Agente de Tecnologia, neste artigo estudaremos o algoritmo ordenação por seleção ou selection sort.

Antes de mais nada, a ordenação de elementos consiste basicamente em colocá-los em ordem crescente ou decrescente. Alguns exemplos de ordenação são: ordenar alunos pelas suas notas; ordenar uma lista telefônica pelo nome das pessoas; ordenar pessoas por idade; ordenar clientes de acordo com a renda; entre outras. 

Além disso, para ordenação dos elementos, podem ser utilizados diversos algoritmos de ordenação, dentre os quais, três deles constam no edital do concurso do Banco do Brasil: método da bolha, ordenação por seleção e ordenação por inserção.

Neste artigo, abordaremos os seguintes tópicos sobre o algoritmo de ordenação por seleção:

• Entendendo o algoritmo de ordenação por seleção: etapas
• Pseudocódigo do algoritmo de ordenação por seleção
• Exemplo (passo a passo)
• A não estabilidade do algoritmo de ordenação por seleção
• Análise de complexidade do algoritmo de ordenação por seleção
• Resumo
• Vamos praticar!

Entendendo o algoritmo de ordenação por seleção: etapas

Primeiramente, para ordenar uma lista, o algoritmo de ordenação por seleção funciona, inicialmente, selecionando o menor valor da lista e trocando com o primeiro elemento. Em seguida, como o primeiro elemento já está em sua posição, o algoritmo seleciona o menor elemento do restante da lista e troca com o primeiro elemento deste restante. 

E isso acontece em cada iteração, com a lista restante ficando um elemento menor que na iteração anterior e a primeira parte da lista ficando ordenada. Este processo ocorre até que todos os elementos sejam comparados e, consequentemente, ordenados.

Para facilitar o entendimento, vejamos as etapas do algoritmo de ordenação por seleção:

1. Receber uma lista de entrada;
   
2. Encontrar o menor elemento da lista e trocá-lo com o primeiro elemento. Este elemento estará ordenado.
   
3. Considerar apenas o restante da lista que não está ordenado e ir para o passo 2.
   
4. Quando o restante da lista estiver vazio, então a lista estará ordenada.
   

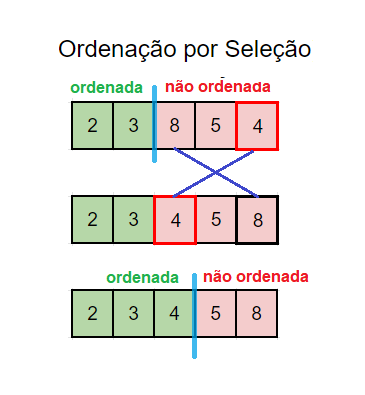
Observe que o que o algoritmo de ordenação por seleção faz é basicamente dividir a lista principal em duas sub-listas, uma ordenada e a outra desordenada. Inicialmente, a lista ordenada começa vazia e a lista desordenada com todos os elementos da lista principal. Ao longo do tempo, a lista ordenada vai crescendo e a desordenada diminuindo, considerando que a junção das duas equivale à lista principal.

Pseudocódigo do Algoritmo de Ordenação por Seleção

A divisão lógica em sub-listas ordenada e não ordenada é utilizada apenas para fins didáticos, para facilitar o entendimento. Assim, o que o algoritmo faz na verdade é percorrer a lista e a cada iteração ir colocando os menores elementos à esquerda. 

Assim, na primeira iteração, o menor elemento é selecionado e vai para a primeira posição; na segunda iteração, ignora-se o primeiro elemento, e seleciona-se o menor entre o restante da lista, que vai para a segunda posição; e assim por diante, até a última iteração. 

Abaixo está o pseudocódigo do algoritmo de ordenação por seleção e, logo após, a explicação de cada linha:

Vejamos, então, a explicação do pseudocódigo:

• Primeiramente, o algoritmo recebe o vetor não ordenado com n elementos.
  
• Em seguida, o algoritmo realiza um loop através dos elementos do vetor, desde o primeiro até o penúltimo, já que a penúltima iteração ordenará os dois últimos elementos, trocando-os de posição, se for o caso.
  
• A cada iteração, a variável min, que representa o índice do menor elemento, é inicializada com o índice atual, i.
  
• Dentro do segundo loop, o algoritmo percorre o restante do vetor a partir do elemento seguinte ao elemento atual, procurando o menor elemento. Perceba, então, que os elementos já ordenados não fazem mais parte das comparações realizadas.
  
• Se um elemento menor for encontrado, o índice min é atualizado com o índice do elemento encontrado.
  
• Por fim, se o índice min for diferente de i, o algoritmo troca o elemento no índice i com o elemento no índice min, colocando o menor elemento encontrado na posição correta.
  
• Depois que todos de percorrer todos os elementos e realizar as comparações, a lista estará ordenado.

Exemplo de ordenação com o algoritmo de ordenação por seleção: passo a passo

Para exemplificar, iremos considerar a seguinte lista: [8, 4, 2, 5, 3]. Inicialmente, temos toda a lista fora de ordem. Dessa forma, a sub-lista ordenada começa vazia e a sub-lista não ordenada começa com todos os elementos.

Primeira iteração

Na primeira iteração temos:

O algoritmo de ordenação por seleção inicia selecionando o menor elemento da sub-lista não ordenada, que é o valor 2, e o troca com o primeiro elemento desta sub-lista, que é o valor 8. Ao fim da primeira iteração, o valor 2, que está ordenado, passa a fazer parte da sub-lista ordenada. Dessa forma, a sub-lista ordenada passa a ter seu primeiro elemento, [2], enquanto que a sub-lista não ordenada diminui um elemento, passando a ser [4, 8, 5, 3].

Segunda iteração

Vejamos, então, a segunda iteração do algoritmo:

Veja que na segunda iteração, o valor 2 já não faz mais parte do processo de seleção, pois está na sub-lista ordenada. Assim, o menor dentre os desordenados é o 3, que é trocado com o primeiro deles, que é o 4. Ao final então temos os valores ordenados [2, 3] e o restante desordenados [8, 5, 4].

Terceira e quarta iterações

Observe que este processo é repetitivo. Sendo assim, para não tornar a explicação repetitiva, apresentamos em conjunto a terceira e a quarta iteração:

Vejamos, então, algumas observações importantes:

• Ao final da terceira iteração a lista já estava ordenada, mas mesmo assim, o algoritmo rodou mais uma iteração. Por esta razão, embora o algoritmo de ordenação por seleção seja simples e fácil de implementar, ele é muito ineficiente, pois roda todas as iterações mesmo se a lista já estiver ordenada.
  
• A última iteração é N – 1, sendo N o tamanho da lista. Isso ocorre porque, em qualquer caso, ao restarem dois elementos, ambos estarão ordenados após a iteração, sem necessitar de uma nova.

Em resumo, o algoritmo de ordenação por seleção funciona selecionando o menor elemento de uma lista não ordenada e colocando-o na primeira posição. Isso é repetido para cada posição subsequente até a lista inteira estar ordenada. É um algoritmo simples, porém ineficiente em termos de tempo de execução, principalmente quando aplicado em grandes conjuntos de dados.

A Não Estabilidade do Algoritmo de Ordenação por Seleção

O algoritmo de ordenação por seleção não preserva a ordem original dos elementos iguais. Essa propriedade é conhecida como estabilidade de um algoritmo de ordenação.

Um algoritmo de ordenação é estável se ele mantém a ordem original dos elementos iguais. Isso significa que, se dois elementos são iguais, e aparecem na ordem original como A e B, então depois de ordenados, eles continuarão aparecendo como A e B, independentemente da ordem em que o algoritmo realiza a comparação deles.

No entanto, o algoritmo de ordenação por seleção não é estável, pois ele escolhe o menor elemento da lista e o coloca na primeira posição, sem levar em consideração a ordem original dos elementos iguais. Isso pode resultar em mudanças na ordem original dos elementos iguais.

Exemplo da não estabilidade do algoritmo de ordenação por seleção

Vejamos um exemplo que mostra como o algoritmo de ordenação por seleção não preserva a ordem original de elementos iguais (neste caso, temos dois elementos de valor 2 colocados em cores diferentes para facilitar o entendimento):

Lista original: (2, 5, 3, 2, 1)

• Na primeira iteração, o algoritmo de ordenação por seleção seleciona o menor elemento da lista, que é 1, e o coloca na primeira posição.
  • A lista agora se torna (1, 5, 3, 2, 2).
    
• Na segunda iteração, o algoritmo seleciona o próximo menor elemento, que é 2, e o coloca na segunda posição.
  • A lista agora se torna (1, 2, 3, 5, 2).
    
• Na terceira iteração, o algoritmo seleciona o próximo menor elemento, que é 2, e o coloca na terceira posição.
  • A lista agora é (1, 2, 2, 5, 3).
    
• Na última iteração, o algoritmo seleciona o próximo menor elemento, que é 3, e o coloca na quarta posição.
  • A lista continua (1, 2, 2, 3, 5)
    

Como podemos perceber, a ordem original dos dois 2’s foi alterada. No início, o 2 azul aparecia antes do 2 vermelho. Entretanto, com a ordenação por seleção, essa ordem mudou. No entanto, se tivéssemos usado um algoritmo de ordenação estável, a ordem original dos 2’s teria sido preservada.

Uma importante observação é que, diferente do algoritmo de ordenação por seleção, os algoritmos de ordenação bolha e por inserção são estáveis, preservando a ordem original dos elementos iguais.

Análise de Complexidade do Algoritmo de Ordenação por Seleção

Um dos pontos importantes no estudo e desenvolvimento de algoritmos é a análise de complexidade dos algoritmos, que é uma forma de calcular o desempenho de um algoritmo através do número de operações realizadas (como comparações, atribuições, etc.) à medida que o tamanho da entrada aumenta.

Assim, com base na análise da complexidade, é possível calcular o tempo de execução de um algoritmo. A análise de complexidade é importante pois permite que entendamos como o desempenho de um algoritmo é afetado pelo tamanho da entrada, possibilitando a escolha de algoritmos mais adequados de acordo com o problema.

De cara, podemos observar que no algoritmo de ordenação por seleção temos um laço de repetição dentro de outro, ou seja, de grosso modo, a lista é percorrida N * N, ou N², sendo N o tamanho da lista. Portanto, a complexidade do algoritmo de ordenação por seleção é n², em todos os casos: pior, médio e melhor.

Quantidade de comparações e trocas realizadas

Além disso, é importante saber o número de comparações e de trocas realizadas. É importante observar que algoritmo realiza, para cada iteração, uma quantidade de comparações diferente, pois o processo de seleção ignora os elementos já ordenados.

Então, considerando uma lista de 5 elementos, temos:

• Primeira iteração: Toda a lista é percorrida, sendo realizadas 4 comparações. Perceba que como são 5 elementos, são necessárias quatro comparações. Portanto, o número de comparações equivale ao tamanho da lista comparada subtraído de um.
  
• Segunda iteração: A lista a ser percorrida para obtenção do menor elemento é considerada a partir do segundo elemento, pois o primeiro já está ordenado. Logo, como são 4 elementos para comparação, realizam-se 3 comparações.
  
• Terceira iteração: Seguindo o mesmo raciocínio, serão realizadas 2 comparações.
  
• Quarta iteração: Por fim, aqui temos 1 comparação.

Dessa forma, realizam-se 4 + 3 + 2 + 1 = 10 comparações.

De forma mais rápida, podemos calcular o número de comparações realizadas pelo algoritmo de ordenação por seleção através da seguinte equação: 

C = n * ( n - 1 ) / 2, onde C é o número de comparações.

 Assim, para uma lista de tamanho 5, o número de comparações é (5 * 4)/2 = 10.

Além disso, é interessante observar que em cada iteração acontece no máximo uma troca de posição na lista, podendo não acontecer nenhuma, caso o menor valor já esteja no início da lista considerada na iteração. Sendo assim, para uma lista de n elementos, como temos n – 1 iterações, teremos, no máximo, n – 1 trocas. Logo:

T ≤ n - 1, onde T é o número de trocas.

Portanto, para uma lista de 5 elementos, teremos, no máximo, 4 trocas com o algoritmo de ordenação por seleção.

Além disso, é importante ressaltar que essas fórmulas são meramente aproximações e que a quantidade real de comparações e trocas pode variar dependendo da implementação do algoritmo.

Resumo com os principais pontos

• O algoritmo de ordenação por seleção funciona selecionando o menor elemento de uma lista não ordenada e colocando-o na primeira posição. Repetindo-se este procedimento para cada posição subsequente até a lista inteira estar ordenada.
  
• É um algoritmo simples, porém ineficiente em termos de tempo de execução, principalmente quando aplicado em grandes conjuntos de dados.
  
• A complexidade do algoritmo é quadrática, ou seja, n², em todos os casos: caso médio, melhor caso e pior caso.
  
• O número de comparações que o algoritmo realiza é C = n * (n – 1) / 2, sendo n o tamanho da lista.
  
• O número de trocas que o algoritmo realiza é T ≤ n – 1, ou seja, o número de trocas é no máximo n – 1.
  
• O algoritmo de ordenação por seleção é não estável, ou seja, não preserva a ordem original dos elementos iguais.

Vamos Praticar!

Enfim terminamos o artigo sobre o algoritmo de ordenação por seleção, espero que este estudo seja útil para sua jornada rumo à aprovação no concurso do Banco do Brasil.

Se preparando para o concurso do Banco do Brasil? Então, confira nossos cursos:

Pacote para o cargo Agente de Tecnologia

Pacotaço (Conteúdo + Passo estratégico) para o cargo Agente de Tecnologia

Quer saber tudo sobre concursos previstos?
Confira nossos artigos!

Concursos abertos

Concursos 2023